Lista 4 – 2020 – UFAM – Cálculo I – Questão 2f
Calcule os seguintes limites. Justifique suas respostas.
f)
Passo 1
Falaeee, beleza??? Seguinte... Se a gente só substituísse o por , apresentaria uma indeterminação do tipo .
E agora, como proceder com isso?? Fica aqui que devagarinho a gente desenrola haha!
Passo 2
Bora começar colocando o termo de com a maior potência em evidência:
OBS: Como pode ser negativo, ele precisa sair da raiz como módulo, ok?
Passo 3
Como irá assumir valores negativos (pois tende a ), sabe-se que . Assim, a gente tem:
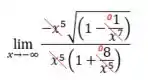
Ou seja, “cortando” esses termos iguais e os outros que tendem a zero, vemos que:
Tranquilo? Responde Aí!! ;)
Resposta
Exercícios de Livros Relacionados
Encontre o limite ou demonstre que não existe. lim x → ∞ 1 - e x 1 + 2 e x
Um tanque contém 5000 l de agua pura. Agua salgada, contendo 30 g de sal por litro de agua é bombeada para dentro do tanque a uma taxa 25 l / m i n . Mostre que a concentração de sal depois det minuto
Encontre o limiteunderset(x - oo)(lim) (x + 2)/(sqrt(9 x^2 + 1))
Encontre o limiteunderset(u - oo)(lim) (4 u^4 + 5)/((u^2 - 2) ( 2 u^2 - 1 ))
Para o limite: lim x → ∞ 2 x + 1 x + 1 = ∞ Ilustre a definição 9, encontrando o valor de N correspondentes a M = 100