Calcule:
(a)
Passo 1
Ver o que acontece no limite indicado
Eu não sei você mas quando eu vejo uma raiz em questões de limite já da arrepios. Mas relaxa que vamos tirar de letra. O primeiro passo é tentar ver o que acontece no limite de para valores infinitamente pequenos. Veja que:
E que:
Graficamente:
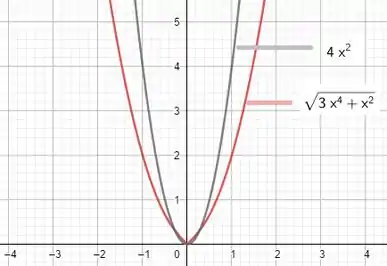
Eita, caímos numa indeterminação então do tipo . Temos que tentar rearranjar então o limite pra mandar essa indeterminação pro espaço.
Passo 2
Colocar o que puder em evidência
Da uma olhada com muito carinho no limite, vê um padrão? Se não, repara que o termo se repete algumas vezes. Vamos colocar ele em evidência então:
Passo 3
Colocar tudo dentro da raiz e aplicar o limite
Opa, mas perai, continuamos com uma indeterminação do tipo , e agora? Calma jovem Padawan! Quando a gente trabalha com quocientes e tem uma raiz, as vezes ajuda se colocarmos tudo dentro da raiz. Sendo:
Nosso limite vai ficar:
Agora sim a indeterminação sumiu! Basta aplicar o limite e partir pro abraço