UFU – Cálculo 1 – Listas – Professor Sato
7.3 Para as funções abaixo, encontre os limites quando (i) e (ii) . Em seguida, determine quais funções admite uma assíntota horizontal. Inclua as equações e os gráficos das assíntotas, bem como um esboço dos gráficos dessas funções indicando o(s) comportamento(s) assintóticos no infinito.
d)
Passo 1
Falaaa... beleza???
Nessa questão vamos calcular o limite de quando tendo a e quando tende a .
Se esses limites derem algum número (que não seja infinito), então vai apresentar assíntota horizontal e esse número vai indicar a reta paralela ao eixo , que a assíntota vai encostar lááá no infinito.
Passo 2
(i) pra tendendo a :
Dividindo por em cima e embaixo:
O que tem embaixo vai pra zero:
Então não tem assíntota quando .
Passo 3
(i) pra tendendo a -:
Dividindo por em cima e embaixo:
O que tem embaixo vai pra zero:
Então não tem assíntota quando .
Para o gráfico temos, a função:
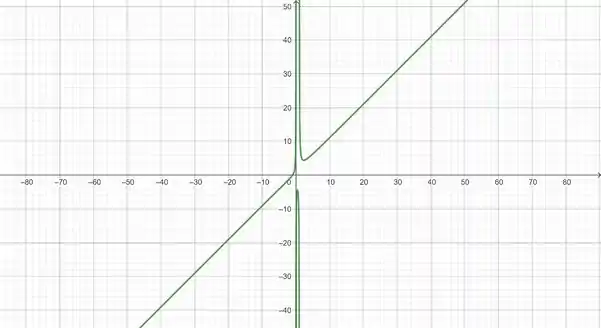
Resposta
Resposta nos passos