Calcule as derivadas:
Passo 1
Fala aí, galerinha! Tudo bem com vocês? Nosso primeiro passo vai ser reescrever nossa função em um formato que nos permita calcular a derivada a partir de derivadas que a gente aprende nos nossos cursos de cálculo, isso porque não sabemos a derivada , certo?
Bora lá, o truque que vamos utilizar e que quase sempre funciona quando a gente encontra expressões como essa da nossa questão onde aparece um no expoente é tentar tirar o logaritmo natural e depois elevar a . Vamos relembrar que e são funções inversas, o que quer dizer que fazer uma operação e depois a outra é o mesmo que fazer nada, seria como se, por exemplo, nós multiplicássemos nossa expressão por e depois dividíssemos por .
Bom, você deve então estar se perguntando: “se tirar o e depois elevar a é o mesmo que fazer nada, o que eu ganho com isso?” Excelente pergunta! Acontece que diferente de , as derivadas de e são duas que nós costumamos aprender e decorar nos nossos cursos de cálculo. Reescrever nossa expressão em função dessas outras duas vai permitir com que a gente determine a derivada geral. Além disso, os logaritmos têm a incrível propriedade de nós podermos pegar um expoente e passar multiplicando para frente, o que facilita muito as nossas vidas! Se liga então:
Passo 2
Beleza! Já reescrevemos nossa expressão em um formato conveniente para calcular a derivada. Agora, o próximo passo é aplicarmos a Regra da Cadeia, que diz o seguinte:
Calma lá! Essa expressão parece complicada, mas vamos destrinchá-la pra gente entender melhor. Nessa questão temos que calcular a derivada de , mas podemos pensar nessa função como a composta de outras duas, conforme ilustrado na figura abaixo:
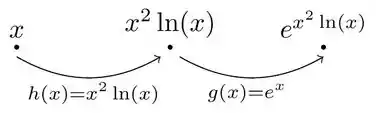
Primeiro nós pegamos nosso número e passamos pela função . O resultado dessa operação, nós aplicamos na função !
Para aplicarmos a Regra da Cadeia, precisamos tanto da derivada de quanto da derivada de . Como a derivada da exponencial é ela mesma, temos:
Agora, para calcular a derivada de , precisamos utilizar a Regra do Produto:
Show! Só nos falta então, para aplicar a Regra da Cadeia completa, calcular quem é :
Mas já vimos no Passo 1 que a expressão acima é equivalente a . Logo:
Finalmente, juntando todos os nossos passos, temos, da Regra da Cadeia:
Passo 3
Beleza, agora que já determinamos a derivada de , só nos resta lembrar que a derivada da soma é a soma das derivadas!
Acabamos! Bora pra próxima questão? 😊