UFRJ – Cálculo 1 – Lista 6 – Questão 3
Considere as funções dadas por e e os valores dados na tabela abaixo, encontre:
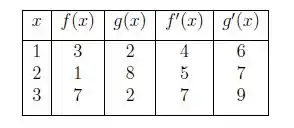
Passo 1
Para resolver esse problema podemos usar diretamente a definição da regra da cadeia, onde temos que:
Logo,
Passo 2
Assim, como queremos , ou seja, a derivada de no ponto 1, é só substituir esse valor na expressão:
Passo 3
Assim, como queremos , ou seja, a derivada de no ponto 1, é só substituir esse valor na expressão:
Resposta
Exercícios de Livros Relacionados
Encontre a derivada da função.y = ((x^2 + 1)/(x^2 - 1))^3
Encontre a derivada da função.(d)/(d x) 2^(sen ( pi x ))
Encontre a derivada da função. y = r r 2 + 1
Encontre a derivada da função. G y = y - 1 4 y 2 + 2 y 5
Encontre a primeira e a segunda derivadas da função. y = e α x β x