USP, Cálculo 1 – P2 – 2021.2 – Questão 2b
Calcule as derivadas:
Passo 1
Opa! Tudo bom? Nossa questão é uma aplicação da Regra da Cadeia, que diz o seguinte:
Mas calma! Essa expressão aqui em cima parece super complicada, mas a gente vai entender tintim por tintim como utilizá-la no nosso caso. O que acontece aqui é que a nossa função é a composta de duas outras funções, como mostrado na figura abaixo:
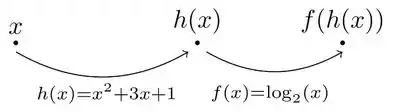
Primeiro nosso passa pela função , que é um polinômio. Em seguida, aplicamos nesse resultado o , que é a função ! O que a Regra da Cadeia nos ensina é como calcular a derivada da função , que é a composta dessas duas.
Bora lá, nosso primeiro passo vai ser então calcular as derivadas de e , que são funções cujas derivadas têm fórmulas fechadas que a gente aprende nos nossos cursos de Cálculo:
e
Passo 2
Beleza! Já calculamos e , mas se repararmos bem, na Regra da Cadeia não aparece , mas sim . Nosso próximo passo é então substituir dentro da :
Passo 3
Show de bola! Agora já temos tudo de que precisamos para aplicar a Regra da Cadeia:
E tá pronto! Vamos pra próxima questão?