Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 871234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586888990919293949596979899100

Enunciado

Uma partícula se move ao longo de reta da origem aos pontos 1 ,   0 ,   0 , 1 ,   2 ,   1 , 0 ,   2 ,   1 , e de volta para a origem sob influência do campo

F → x ,   y ,   z = z 2 ,   2 x y ,   4 y 2 .

  1. Calcule o rotacional do campo F → .
  2. Calcule o trabalho realizado.

Passo 1

a )

Primeiro quem é o rotacional?

r o t   F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y →

Como

F → x ,   y ,   z = z 2 ,   2 x y ,   4 y 2 = F 1 ,   F 2 ,   F 3

Então, pelo cálculo das derivadas parciais...

r o t   F → = 8 y - 0 ,   2 z - 0 ,   2 y - 0 →

r o t   F → = 8 y ,   2 z ,   2 y

Logo, vamos ter que calcular a integral de superfície desse vetor aí! Fique atento para não esquecer e usar F → , heim!

Passo 2

b )

Sabemos que trabalho de uma força F →   sobre uma curva C é dado pela integral de linha:

T r a b a l h o = ∫ C   F → ⋅ d r →

Poderíamos tentar calcular essa integral aí na marra, mas pow! O problema não nos pediu para calcular o rotacional atoa... Ou seja, ele quer e o usemos. E qual teorema relaciona um trabalho com um rotacional? O Teorema de Stokes:

∫ C   F → ⋅ d r → = ∬ S   r o t   F → ⋅ n →   d S

Passo 3

Mas tipo, não podemos sair aplicando essa igualdade assim... De qualquer forma. Devemos averiguar as condições do Teorema que nos exige:

1º - Uma curva fechada C que esteja delimitando uma superfície S .

2º - Um campo sem singularidades F → .

3º - Uma curva e região S orientadas positivamente.

Vejamos essas condições estão sendo satisfeitas então ;)

Passo 4

Quanto à 1 º exigência, bem, ela está sendo satisfeita, pois a curva é fechada. Ora, basta desenha-la para você ver que isso de fato está acontecendo (basta colocar os 4 pontos no espaço e liga-los):

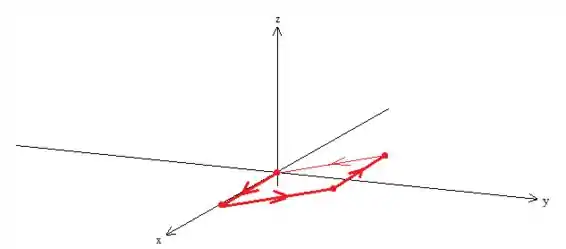
Veja que essa curva está delimitando uma superfície S plana (representado em verdinho):

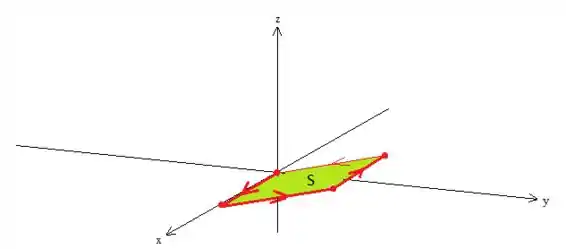
Passo 5

A segunda exigência refere-se ao campo, e bem, ele não tem problema algum, como uma divisão por 0 , ou algo do tipo, veja:

F → x ,   y ,   z = z 2 ,   2 x y ,   4 y 2 .

Passo 6

Já a última condição nos obriga que o conjunto curva e superfície estejam orientadas positivamente. Isso significa que como a curva gira nesse sentido anti-horário vista por cima, a superfície S tem um vetor normal N → associado a esse sentido. Para descobri-lo, basta aplicar a Regra da Mão Direita:

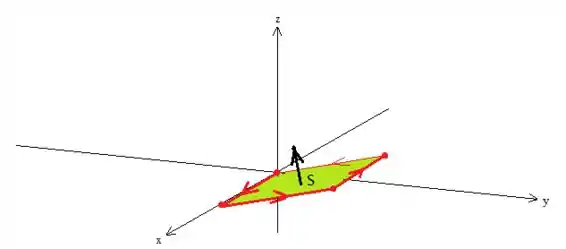
Então o Vetor N → que queremos está pra cima, saca?

Passo 7

Bem, estando nas condições de Stokes, podemos aplicar a igualdade numa boa:

∫ C   F → ⋅ d r → = ∬ S   r o t   F → ⋅ n →   d S

E ao invés de calcularmos uma integral de linha em cima de uma curva que é composta (o que sugere que daria um trabalhão pra gente), podemos simplesmente calcular a integral de superfície em cima do plano, saca?

Agora, para a integral de superfície não tem muito o que fazer e sim calcula-la na marra:

1 º - Parametrizar a superfície S .

2º - Encontrar o rotacional nos termos da parametrização.

3º - Encontrar o termo n →   d S .

Então venha comigo ;)

Passo 8

Bem, primeiro, como vimos, devemos parametrizar a superfície S . Para parametrizar um plano, necessitamos da equação dele em mãos. A equação genérica de um plano é...

A x + B y + C z + D = 0

Onde pra encontrar esses A ,   B ,   C   e D , podemos simplesmente substituir os pontos 1 ,   0 ,   0 , 1 ,   2 ,   1 e a origem também e ver no que encontramos... Observa:

0 ,   0 ,   0       →             A 0 + B 0 + C 0 + D = 0     →

D = 0    

Substituindo o segundo ponto...

1 ,   0 ,   0         →           A 1 + B 0 + C 0 = 0     →

A = 0  

e o último...

1 ,   2 ,   1         →           B 2 + C 1 = 0     →

2 B + C = 0     →           C = - 2 B

Substituindo tudo na equação do plano...

0 x + B y + - 2 B z + 0 = 0   →

B y - 2 z = 0

Se o B não for zero (se fosse não teria plano), o plano é um múltiplo de...

y - 2 z = 0

Sacou?

Passo 9

Parametrizar um plano, que tem uma equação explícita, pode ser feito utilizando a parametrização explícita...

                                          x = u

                                            y = v

y - 2 z = 0       →       z = y 2 = v 2

Com uma notação um pouco mais gentil...

r → u ,   v = u ,   v , v 2

Como saímos da origem e fomos até 1 ,   0 ,   0 , ou seja, andamos penas 1 unidade em x , isso sugere que...

0 ≤ x ≤ 1 →

0 ≤ u ≤ 1

Depois sem andar em x , saímos de 1 ,   0 ,   0 e fomos até 1 ,   2 ,   1 , logo andamos duas unidades (saindo do 0 ) para y ...

0 ≤ y ≤ 2 →

0 ≤ v ≤ 2

Passo 10

Substituindo os termos das parametrizações no rotacional (o qual queremos a integral de superfície):

r o t   F → = 8 y ,   2 z ,   2 y

r o t   F → r → u ,   v = 8 v ,   v ,   2 v

Passo 11

Calculando por último antes de voltar para a integral de superfície e superfície e matar o problema a termo n →   d S :

n → d S = N →   d u d v

Onde esse vetor normal é dado por...

N → = ∂ r → u ,   v ∂ u × ∂ r → u ,   v ∂ v

Mas como estamos utilizando uma parametrização como gráfico de função...

z = v 2

Podemos calcular N → pelo bizu...

N → = - ∂ z ∂ u ,   - ∂ z ∂ v , 1

Então

N → = 0 ,   - 1 2 ,   1

Que é justamente o Vetor que precisamos, pois obedece a condição do orientada positivamente :D!

Logo

n → d S = 0 ,   - 1 2 ,   1   d u d v

Passo 12

Substituindo tudo na integral de superfície:

∬ S   r o t   F → ⋅ n →   d S =

∫ 0 2 ∫ 0 1 8 v ,   v ,   2 v ⋅ 0 ,   - 1 2 ,   1 d u d v =

∫ 0 2 ∫ 0 1 - v 2 +   2 v   d u d v = ∫ 0 2 ∫ 0 1 3 v 2   d u d v

Integrando...

∫ 0 2 3 v 2 ∫ 0 1   d u d v = ∫ 0 2 3 v 2 d v =

3 2 v 2 2 0 2 = 3 2 2 2 2 =

3

Então pelo teorema de Stokes:

T r a b a l h o = ∫ C   F → ⋅ d r → = 3

Resposta

a )   r o t   F → = 8 y ,   2 z ,   2 y

b )   3

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê