Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 751234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 3, lista 3 - 2021.1, Questão 12b

( b ) Seja γ a curva de intersecção do prisma (superfície) de faces x = 2 , x = - 2 , y = 3 , y = - 3 , com o plano z = - x + 4 , orientada de modo que sua projeção no plano x y seja percorrida no sentido anti-horário. Calcule ∫ γ [ - ( y - 1 ) x 2 + ( y - 1 ) 2 ] d x + [ x x 2 + ( y - 1 ) 2 + z ] d y + s e n ( z ) d z .

Passo 1

Eaew, belezinha?

O enunciado nos pede para calcularmos a seguinte integração

∫ γ [ - ( y - 1 ) x 2 + ( y - 1 ) 2 ] d x + [ x x 2 + ( y - 1 ) 2 + z ] d y + s e n ( z ) d z

e indica que a curva γ pode ser obtida através da intersecção do prisma que tem faces em

x = 2 , x = - 2 , y = 3 e y = - 3

com o plano z = - x + 4 para isso, vamos utilizar o teorema de Stokes que faz a seguinte identificação

∫ γ F → ⋅ d r → = ∫ ∫ S r o t ( F → ) ⋅ n →   d S

em que

F → = [ - ( y - 1 ) x 2 + ( y - 1 ) 2 , x x 2 + ( y - 1 ) 2 , s e n ( z ) ]

Consegue ler a definição acima? Se não, vem comigo!

Passo 2

A primeira coisa que precisamos fazer é verificar quem é a curva γ , se ignorar a escala do gráfico a seguir, podemos visualizar que a nossa curva gamma é tal que

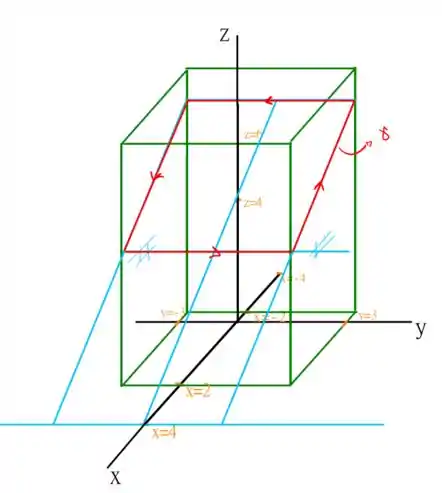
Ou seja, ela é a curva fronteira de um plano! Note que é o próprio plano que foi dado no enunciado! Isso nos é útil, pois podemos utilizá-lo como a superfície na integral dupla do teorema de Stokes! Vamos então calcular todos os termos necessários!

Passo 3

Vamos calcular as grandezas no lado direito do teorema de Stokes! Podemos começar com

r o t ( F → ) = ∇ → × F →

usando que ∇ → = ( ∂ ∂ x , ∂ ∂ y , ∂ ∂ x ) , e usando a fórmula para o produto vetorial, temos

r o t ( F → ) = ( ∂ F z ∂ y - ∂ F y ∂ z , ∂ F x ∂ z - ∂ F z ∂ x , ∂ F y ∂ x - ∂ F x ∂ y )

precisamos calcular todas as derivadas parciais! Vamos fazer uma de cada vez

∫ γ [ - ( y - 1 ) x 2 + ( y - 1 ) 2 ] d x + [ x x 2 + ( y - 1 ) 2 + z ] d y + s e n ( z ) d z

∂ F z ∂ y = ∂ ∂ y [ s e n ( z ) ]

como temos a derivada parcial em y , tudo que não depende de y é uma constante, temos então que

∂ F z ∂ y = 0

já que a função não depende de y . Analogamente, vamos calcular as outras derivadas parciais

∂ F y ∂ z = ∂ ∂ z [ x x 2 + ( y - 1 ) 2 + z ] = 1

∂ F x ∂ z = ∂ ∂ z [ - ( y - 1 ) x 2 + ( y - 1 ) 2 ] = 0

∂ F z ∂ x = ∂ ∂ x [ s e n ( z ) ] = 0

∂ F y ∂ x = ∂ ∂ x [ x x 2 + ( y - 1 ) 2 + z ]

∂ F x ∂ y = ∂ ∂ y [ - ( y - 1 ) x 2 + ( y - 1 ) 2 ]

As duas últimas derivadas vão nos dar um trabalhinho a mais! Vamos fazer elas separadamente!

Passo 4

Ambas vão usar a regra do quociente, mas lembre-se que os termos que não dependem da variável são todos constantes, portanto, temos que

∂ ∂ x [ x x 2 + ( y - 1 ) 2 + z ] = x 2 + ( y - 1 ) 2 - x [ 2 x ] [ x 2 + ( y - 1 ) 2 ] 2 + 0 = ( y - 1 ) 2 - x 2 [ x 2 + ( y - 1 ) 2 ] 2

analogamente, temos que

∂ ∂ y [ - ( y - 1 ) x 2 + ( y - 1 ) 2 ] = - x 2 - ( y - 1 ) 2 + 2 ( y - 1 ) 2 [ x 2 + ( y - 1 ) 2 ] 2 = ( y - 1 ) 2 - x 2 [ x 2 + ( y - 1 ) 2 ] 2

Portanto, nosso rotacional será

r o t ( F → ) = ( 0 - 1,0 - 0 , ( y - 1 ) 2 - x 2 [ x 2 + ( y - 1 ) 2 ] 2 - ( y - 1 ) 2 - x 2 [ x 2 + ( y - 1 ) 2 ] 2 )

ou simplificando o último termo, temos que

r o t ( F → ) = ( - 1,0 , 0 )

Ótimo! O rotacional ficou razoavelmente simples! Agora, precisamos do nosso vetor normal! Vamos lá!

Passo 5

O vetor normal pode ser obtido através da equação do plano

z = - x + 4

note que a equação geral do plano é

a x + b y + c z + d = 0

em que n → = ( a , b , c ) é o vetor normal ao plano. Portanto, temos que o vetor normal em nosso caso é

x + z - 4 = 0

Portanto, n → = ( 1,0 , 1 ) . Vamos escrever agora a nossa integração!

Passo 6

A integral é tal que

∫ γ F → ⋅ d r → = ∫ ∫ S r o t ( F → ) ⋅ n →   d S

temos que a parametrização foi feita em ( u , v ) , portanto d S = d u d v , ou seja

∫ γ F → ⋅ d r → = ∫ ∫ S ( - 1,0 , 0 ) ⋅ ( 1,0 , 1 ) d S = - ∫ ∫ S d S

Isso é simplesmente a área de nossa superfície! Que é um plano, ou seja, a área é a área de um retângulo, olhando a nossa figura vemos que uma dos lados tem tamanho

b = 3 - ( - 3 ) = 6

Para encontrar o outro lado do retângulo vamos ter que analisar o seguinte triângulo

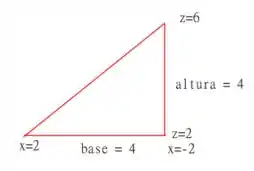
Portanto, usando pitágoras, temos que o outro lado de nosso retângulo tem o tamanho

a = 4 2 + 4 2 = 4 2

e, portanto, temos que a nossa integral é simplesmente

∫ γ F → ⋅ d r → = - 24 2

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

∫ γ F → ⋅ d r → = - 24 2

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê