USP, Sem Campus, Cálculo 3, lista 3 - 2021.1, Questão 7
Suponha que a superfície seja o gráfico de uma função de classe , orientada de modo que a sua normal unitária tenha a terceira componente não negativa. Se é um campo de vetores sobre , mostre que
Passo 1
Eaew, belezinha?
O enunciado nos dá algumas definições bastantes gerais! Temos uma função definida através de
ou seja, uma função que leva um par de variáveis a um valor real! Esta função é de classe , ou seja, é contínua e diferenciável ao menos uma vez, e ela representa o gráfico de uma superfície orientada tal que o vetor normal tenha a terceira componente não negativa. O enunciado também nos dá um campo vetorial da forma
e pede para demonstrar que
Isso pode ser feito escolhendo uma parametrização e escrevendo o nosso vetor normal neste sistema de coordenadas! Em geral, o vetor normal é dado por
Parece complicado? Mas se formos com cuidado vai dar tudo certo! Saca só!
Passo 2
A primeira coisa que podemos fazer aqui é escolher uma parametrização! Para esse caso em particular, temos a facilidade de poder utilizar as coordenadas cartesianas! De forma que podemos usar uma parametrização da forma
em que é a função indicada no enunciado! Note que usando esta parametrização, devemos escrever o nosso elemento de superfície como
em que o elemento é o jacobiano da mudança de coordenadas! Mais uma vez, convenientemente, não precisamos calcular isso! Já que na expressão do vetor normal, iremos eliminar o jacobiano da jogada! Temos que
ou, simplificando, temos que
Ótimo! Agora só precisamos escrever quem são e ! Bora lá!
Passo 3
Os vetores e são
e
calculando as derivadas parciais, nós obtemos que
e
Se calcularmos o produto vetorial entre eles usando a definição em termos do determinante da seguinte matriz
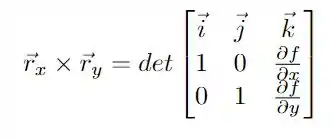
calculando o determinante, obtemos que
Maravilha! Vamos usar isso dentro de nossa integral de superfície!
Passo 4
Podemos substituir o vetor que calculamos no passo anterior na integral para obter
calculando o produto escalar, conseguimos finalmente mostrar que
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!