Seja o campo , tal que , onde é de classe com . Calcule , onde é a curva dada pela interseção das superfícies e , orientada no sentido anti-horário quando vista de cima.
Passo 1
Vamos lá, galera, essa questão aqui tem que ter umas sacadas, vamos prestar bastante atenção nesse passo aqui pra entender tudo! Temos um campo que não sabemos quase nada sobre ele, sabemos apenas que seu rotacional é . E mesmo assim dentro dele ainda tem uma função que só sabemos um ponto.
Ele pede a integral de linha de uma curva , como temos o rotacional, isso nos sugere aplicar o teorema de Stokes. Antes de mais nada, vamos visualizar essa curva , ela é assim
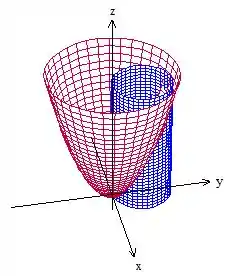

Para aplicar o teorema de Stokes, precisamos escolher uma superfície que possua como fronteira essa curva . A que pensamos primeiro geralmente é simplesmente preencher esse círculo ai e partir pro abraço, nessa questão aqui não vai ser bem assim. Como só sabemos o rotacional de no plano , vamos tentar escolher uma superfície que esteja nesse plano ou que possua normal no eixo igual a zero.
Ué? Porque exatamente essas características? Perceba que, se a normal for algo , quando fizermos o produto escalar disso com o rotacional, aquela função vai sumir! Ou então, quando , sabemos que , então não é problema!
Ah entendi! Mas que superfície tem essas características? Não vai ser uma, mas sim a união de duas superfícies: o cilindro
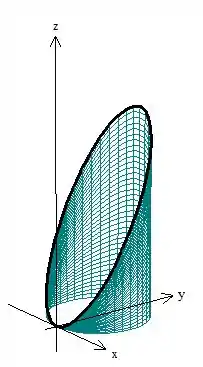
E, o circulo em , assim:
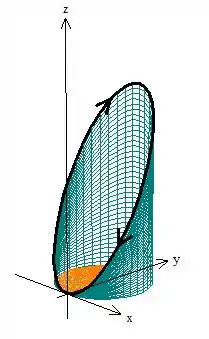
Perceba outro detalhe importante, para a superfície estar à esquerda da curva, precisamos andar no sentido mostrado no gráfico acima, que é o sentido horário visto de cima. A questão pede pra fazermos a curva no sentido anti-horário, portanto o resultado que acharmos temos que inverter o sinal.
Pra concluir essa organização da questão, o teorema de Stokes fica
Passo 2
Vamos começar então pela nossa superfície . Ela é um cilindro deslocado da origem de raio , vamos parametrizá-la da seguinte forma
Só que perceba que é limitado em cima pelo paraboloide , portanto os limites de e vão ser esses aqui
Substituindo os parâmetros
Definidos os parâmetros, precisamos substituí-los no rotacional e encontrar a normal
Passo 3
Vamos começar pelo mais simples, só substituir os parâmetros no rotacional
Deixa esse por ai, ele não vai ser problema lá na frente!
Passo 4
Vamos agora encontrar a normal à superfície, sua fórmula é
Para verificar se os sinais estão corretos, basta pegar algum ponto e ver graficamente se está correto. Quando , o cilindro está no ponto e em qualquer altura e a normal está apontando para fora com o valor de , portanto os sinais estão corretos.
Passo 5
Vamos juntar tudo isso na integral de
Aqui a nossa função some da integral! Fica assim
Vamos integrar cada um desses termos ai
Todas as funções trigonométricas aqui, quando integradas, vão ser iguais a zero, pois e , portanto sobra
Passo 6
Vamos agora para a segunda superfície, . Ela é o círculo em , sua parametrização vai ser essa aqui
Passo 7
Vamos calcular agora a normal dessa superfície
Perceba que a normal está apontando para baixo, então está na direção correta!
Passo 8
Vamos substituir os parâmetros no nosso rotacional
Perceba que, como a normal tem valor zero nos eixos e , só precisamos do rotacional no eixo !
Passo 9
Substituindo isso na integral de superfície
Passo 10
Por fim, juntando tudo no teorema de Stokes
Como queremos a integral da curva , precisamos inverter esse sinal ai, portanto