Calcule onde , é formada pelas cinco faces do cubo que não estão no plano com exterior a , usando o teorema de Stokes.
Passo 1
Ele está mandando usarmos o teorema de Stokes, então quem somos nós para não fazer isso não é mesmo? Mas antes de aplicar o teorema de Stokes temos que entender qual a fronteira desse cubo. Repara que vai ser uma figura assim no
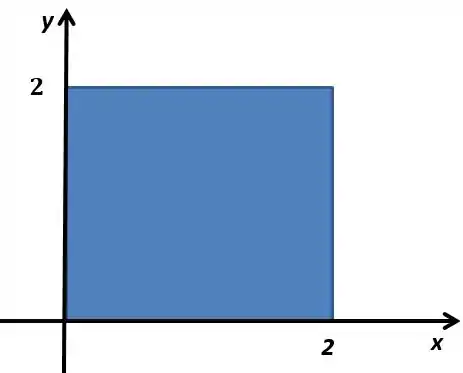
Podemos entender a fronteira como os lados do quadrado, Vamos chamar esses lados de , , e , e fazer
O teorema de Stokes transforma integral de linha em integral dupla através do rotacional, então seria algo assim
E agora que temos podemos usar o teorema de Stokes e calcular a integral de linha
Fica atento que eu não disse quem era qual , mas temos que fazer essa parada rodar no sentido anti-horário.
Passo 2
Vamos fazer de cada lado, primeiro , mas que é ?tanto faz rs vamos fazer o lado que e vai de à
Vamos fazer a parametrização disso
Com
Precisamos agora de
Repara que pegamos o sentido contrário ao que queremos, basta no final da resposta trocar o sinal do cara.
Passo 3
A integral de linha em vai ficar
Como queremos o sentido contrário deveríamos trocar o sinal, mas deu então não faz diferença rs.
Passo 4
Vamos ver agora , aqui vamos deixar e variando entre e
Vamos fazer a parametrização disso
Com
Precisamos agora de
Passo 5
A integral de linha em vai ficar
Passo 6
Vamos ver agora , aqui vamos deixar e variando entre e
Vamos fazer a parametrização disso
Com
Precisamos agora de
Passo 7
A integral de linha em vai ficar
Passo 8
Vamos ver agora , aqui vamos deixar e variando entre e
Vamos fazer a parametrização disso
Com
Precisamos agora de
Repara que pegamos o sentido contrário ao que queremos, basta no final da resposta trocar o sinal do cara.
Passo 9
A integral de linha em vai ficar
E o sinal já está trocado como deveria, desde o início coloquei a integral com na frente
Passo 10
A integral de linha vai ficar
Assim vamos ter