Calcule , onde e é a interseção do cilindro com o plano orientada no sentido anti-horário quando vista de cima
Passo 1
Vamos lá galera, essa questão tem muita letra, vamos nos organizar aqui pra não perder o que é constante e o que é variável. Nosso campo é relativamente complexo, né? Mas perceba que seu rotacional não vai ser!
Ótimo! Com esse rotacional fica muito fácil aplicar o teorema de Stokes. Vamos então escolher a nossa superfície a partir do esboço da curva
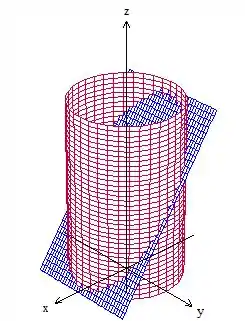
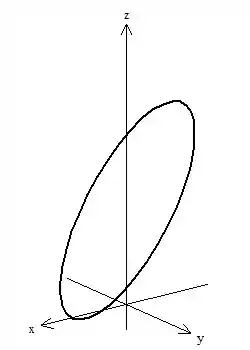
Tendo essa curva, como nosso rotacional é simples, vamos escolher a região de dentro mesmo, nossa superfície vai ser essa aqui
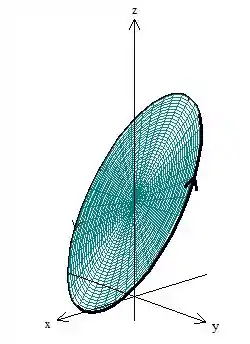
A rotação já está no sentido anti-horário como pediu o enunciado, então, pelo teorema de Stokes
Passo 2
Já temos o rotacional de , precisamos agora de uma parametrização de para calcular seu vetor normal e seus limites. Essa superfície pode ser descrita como um círculo em , portanto
O parâmetro de vai ser um pouco mais complicado. Perceba que é igual ao valor dele no plano , certo? Isolando nessa equação ficamos com
Então a parametrização de vai ser essa aqui
Parece meio complicado, né? Mas nosso rotacional é extremamente simples, então vamos ter um pouco de trabalho nas contas agora do vetor normal, mas na hora de integrar vai ser bem simples, prometo!
Passo 3
Vamos ao cálculo do vetor normal, ele é dado pelo produto vetorial
Vamos ver cada uma dessas derivadas com calma separadas
Beleza, agora vamos pro produto vetorial
Veja que a normal no eixo vai zerar, o que é esperado, já que o plano possuir componentes
Passo 4
Voltando pra integral