Use o teorema de Stokes para calcular em cada um dos seguintes casos:
e é a intersecção da esfera com o plano , orientada de modo que sua projeção no plano seja percorrida no sentido anti-horário.
Passo 1
Oiie, tudo bem com você?
Precisamos usar o teorema de Stokes para calcular a seguinte integral de linha
em que o campo vetorial é dado por
e é a interseção da esfera com o plano , e a orientação é dada de forma que a projeção no plano desta curva esteja orientada no sentido anti-horário. Bem… ele é bem claro no que quer! Mas quem é o teorema de Stokes? Ele é a seguinte identificação
Já que ele quer que calculemos o lado direito da expressão acima usando o teorema, vamos expandir o lado esquerdo! Ou seja, calcular o rotacional, o vetor normal e integrar sobre uma região! Vem comigo!
Passo 2
Primeiro, vamos calcular o rotacional de nosso campo como
percebendo que nosso campo tem o formato , temos que
Agora, precisamos do nosso vetor normal, para isso, vamos analisar a curva dada, temos as seguintes superfícies se interceptando
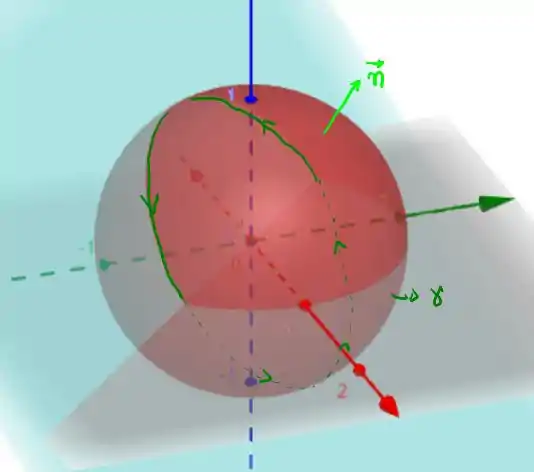
note que a superfície fechada que tem como borda a curva é a própria esfera! Podemos parametrizar a esfera em coordenadas esféricas, de forma que
Vamos usar isso para calcular o nosso vetor normal! Saca só!
Passo 3
O vetor normal pode ser obtido fazendo o seguinte cálculo
em que a parametrização em coordenadas esféricas que fizemos no passo anterior, calculando as derivadas parciais, temos que
e, da mesma forma
calculando o produto vetorial entre os dois vetores, iremos obter que
Ou seja, o produto escalar que está em nosso integrando se torna
resultando em
Maravilha! Agora só precisamos usar esse resultado em nossa integração! E, ver o tamanho do problema em que nos metemos! Bora lá!
Passo 4
Usando o elemento de superfície em coordenadas esféricas [note que não aparece o jacobiano neste caso, pois ele já está incluso no cálculo do vetor normal usando a parametrização, belezinha?], temos que , e se observar a figura, irá notar que e que se fizermos a interseção entre o plano e a esfera, temos que
distribuindo o quadrado e simplificando, temos que
Usando a definição em coordenadas esféricas, temos que
a variação de independe de qual estamos considerando, portanto, vamos usar qualquer , em particular , temos que
Portanto, temos que
ou . Como temos que a esfera começa em ângulos , iremos tomar que . Portanto, temos que
Como os limites de integração são todos constantes, podemos escrever as integrais acima da seguinte maneira
Vamos resolver uma variável por vez! Tenha fé! Bora Bora!
Passo 5
Começando com as integrais em , temos primeiro
para essa integral é conveniente usar a relação de meio ângulo para o seno, ou seja, escrever a integral como
Essas integrais podem ser identificadas como
e, a outra como
ou seja, temos que
Agora, a outra integral em é tal que
aqui é conveniente fazer a substituição simples
e
de forma que obtemos a seguinte integral
em que usei que e , essa integral pode ser identificada como
Portanto, temos que
Ótimo! As integrais em já eram! Agora vamos para as integrais em !
Passo 6
Substituindo os resultados do passo anterior, temos que
Aqui temos integrações mais simples que as anteriores, nós podemos identificar que
e, lembrando que
e, também
ou simplesmente
e, portanto, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!