Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 106123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

11) Seja T o tetraedro de v��rtices O = 0 ,   0 ,   0 , A = 2 ,   0 ,   0 , B = 0 ,   6 ,   0 e C = 0 ,   0 ,   2 . Sejam S a superfície lateral de T , constituída pelas faces de T que não estão no plano x y e F → x ,   y ,   z = 3 y + z ,   x + 4 z ,   2 y + x um campo vetorial R 3 . Calcule ∬ S   r o t   F → ⋅ n →   d S , com a normal exterior a S .

Passo 1

Bem, vamos com calma aqui. Queremos calcular:

∬ S   r o t   F → ⋅ n →   d S

Em cima de S que nos representa um “pedaço” do tetraedro T :

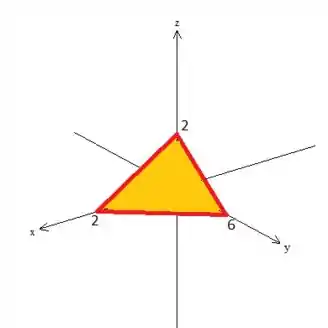
Digo um pedaço, pois estamos falando apenas das três faces que não é a face triangular que está no plano x y , ou seja, é uma superfície aberta.

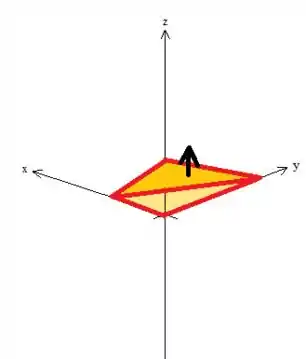
Essa integral de superfície é típica de problema de Stokes e é justamente ele que vamos tentar utilizar aqui, já que de acordo com esse Teorema, podemos aplicar

∬ S   r o t   F → ⋅ n →   d S = ∫ ∂ S   F → ⋅ d r →

Onde essa integral de linha é calculada na borda de S , ou seja, nas retas que está no plano x y , saca? Essas daqui oh:

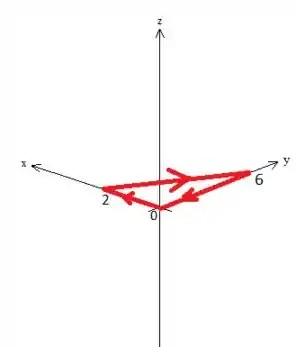
Não sei você, mas eu não quero calcular a integral de linha em cima dessas curvas aí não! Ora, vai dar mais trabalho, pois são muitas curvas (três é muito pra mim). Então o que acha de tentar voltar pra integral de superfície?

Passo 2

Sim, vamos retornar a integral de superfície, mas não pra aquela dali em S :

∬ S   r o t   F → ⋅ n →   d S

O teorema de Stokes é legal com a gente. Ele fala que a gente pode calcular a integral de superfície em qualquer superfície desde que a superfície escolhida tenha como borda a curva que eu te mostrei:

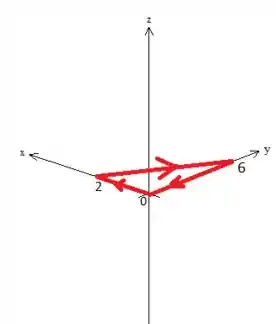
Ora, e qual superfície, além de S , que tem como borda esse cara? O próprio triângulo no plano x y ! :D

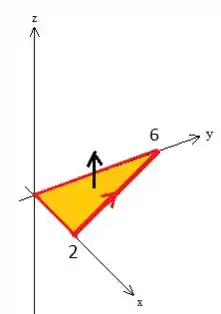
Então, chamando esse plano de superfície 2 , S 2 , pelo teorema de Stokes...

∫ ∂ S   F → ⋅ d r → = ∬ S 2   r o t   F → ⋅ n →   d S

Logo...

∬ S   r o t   F → ⋅ n →   d S = ∬ S 2   r o t   F → ⋅ n →   d S

Veja que ironia nessa última igualdade. Nós queríamos calcular uma integral de superfície em cima de uma superfície que não continha o triângulo em x y , mas por Stokes calcular a integral em cima desse plano é o mesmo que calcular em cima das outras três faces!

Doideira, neh? Então bora comigo calcular essa integral em S 2 :D

Passo 3

Primeiro quem é o rotacional?

r o t   F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y →

Como

F → x ,   y ,   z = 3 y + z ,   x + 4 z ,   2 y + x = F 1 ,   F 2 ,   F 3

Então, pelo cálculo das derivadas parciais...

r o t   F → = 2 - 4 ,   1 - 1 ,   1 - 3 →

r o t   F → = - 2 ,   0 ,   - 2

Logo, vamos ter que calcular a integral de superfície desse vetor aí! Fique atento para não esquecer e usar F → , heim!

Passo 4

Tá, agora quem é a superfície S 2 ? Ora é o triangulo no plano x y , neh:

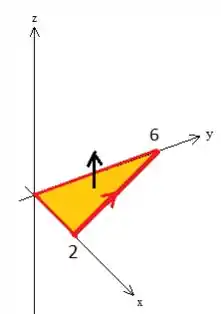
Veja que esse plano tem o vetorsinho normal n → apontando justamente pra cima, logo ele tem coordenadas:

n → = 0 ,   0 ,   1

Esse vetor é justamente o vetor pedido no problema, já que ele aponta pra cima, logo...

∬ S 2   r o t   F → ⋅ n →   d S = ∬ S 2   - 2 ,   0 ,   - 2 ⋅ 0 ,   0 ,   1   d S =

- 2 ∬ S 2     d S =

Veja bem, a chegamos na integral de superfície de 1 d S , que nada mais é do que a área da superfície S 2 ...

- 2 Á r e a   d e   S 2 =

Como a superfície é tranquila (um triângulo) sua área é conhecida: b ase vezes a h altura sobre 2 ...

- 2 b × h 2 =

A base é conhecida e a altura são conhecidas pelo desenho do triângulo:

b = 2

h = 6

Logo...

- 2 2 × 6 2 = - 12

Passo 5

Veja bem, encontramos o valor da integral em S 2 . Mas como vimos...

∬ S   r o t   F → ⋅ n →   d S = ∬ S 2   r o t   F → ⋅ n →   d S

Então

∬ S   r o t   F → ⋅ n →   d S = - 12

Resposta

- 12

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê