Seja a parte do paraboloide que se encontra dentro do cilindro , orientado para cima.
a) Esboçar a superfície .
b) Considere o campo vetorial , usando o Teorema de Stokes, calcular
Passo 1
a) Fala! Vamos esboçar essa bonita
Isso é um paraboloide elíptico virado para cima que começa na origem. Mas ele está dentro do cilindro:
Esse cilindro tem raio , e está centrado na origem. Se a gente desenhar essas duas coisinhas no mesmo espaço:
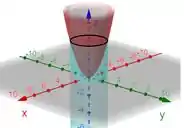
Passo 2
Se é a parte do paraboloide dentro do cilindro, a fronteira de , será essa circunferência preta paralela a , que é a interseção dele com o cilindro.
Como é essa curva? A projeção dela no plano vai ser dada pela mesma equação do cilindro, e para descobrir a altura em que ela está, a gente calcula o da interseção entre:
Nossas superfícies. Daí a gente tira que
Agora, para esboçar finalmente, a gente desenha um paraboloide que vai até a altura . Fica assim:
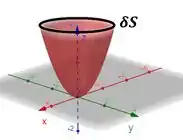
Passo 3
b) Cara, ele pediu para a gente calcular uma integral de linha sobre essa fronteira de , usado o Teorema de Stokes.
Falou de Stokes, primeira coisa a fazer é calcular o rotacional do nosso campo! Ele tem essa fórmulinha:
Nosso campo é:
Então precisamos calcular:
Com esse carinha calculado, vamos seguir! Vem comigo!
Passo 4
O Teorema de Stokes diz que:
é a nossa circunferência paralela ao plano , de raio e que está na altura . Ela é curva que é fronteira da nossa superfície , o paraboloide.
Aquele ali é a superfície de qual a nossa curva é fronteira. E a gente super pode usar o paraboloide mesmo, porque ele é limitado pela fronteira , tá bem?
Maaaas, a gente não precisa usar ele. Como assim? Cara, esse do Teorema pode ser qualquer superfície que tenha nossa circunferência como fronteira, não necessariamente o paraboloide. E isso pode facilitar nossa vida!

A gente vai precisar calcular uma integral de superfície, então faz sentido escolher uma superfície mais simples. Que tal um plano? Nossa, ótima ideia!
Como nossa curva é paralela ao plano , ela está contida num plano paralelo a ele. Vimos que esse é o plano .
Mas ele precisa estar dentro da nossa circunferência. Então a nossa superfície para o Teorema vai ser uma espécie de círculo de raio na altura .
Aí a gente reescreve nossa equação assim:
Então a ideia é que a gente só precisa montar e calcular a integral da direita, para então achar o valor da esquerda. Maneiro, né?
Passo 5
Maaas a gente precisa atender a alguns critérios para podermos aplicar esse teorema antes de começar:
1. Nossa fronteira precisa estar orientada positivamente em relação a superfície.
Como a gente tem uma circunferência e um plano dentro dela, tudo o que a gente precisa é essa circunferência seja percorrida no sentido anti-horário, e que o vetor normal ao plano esteja virado para cima.
Por que? Ao percorrer essa curva com a cabeça no sentido do vetor normal e olharmos para a esquerda, precisamos estar vendo a superfície que limitamos (o plano). E isso acontece nessa situação.
Tipo nesse caso genérico. Vemos isso pela regra da mão direita.
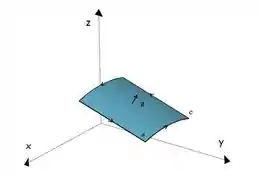
2. O campo precisa estar bem definido para o domínio de integração. Olha ele:
Não tem nenhum ponto de descontinuidade aí né (nenhum denominador que possa zerar ou algo assim). Então a gente pode confiar que ele está bem definido para o nosso domínio de integração, já que ele está bem definido para todos os valores de .
Então, tá belezinha, a gente pode usar o teorema sem preocupações. Bora lá!
Passo 6
Vamos começar parametrizando o plano dentro da circunferência, porque estamos montando uma integral de superfície.
A gente pode parametrizar ele assim:
A componente dele em é porque ele está em no espaço.
E já que ele está limitado pela circunferência que tem projeção em dada por , a gente pode escrever que nosso domínio é:
Como esse é o domínio da parametrização, também será o domínio da nossa integral.
Passo 7
Depois a gente precisa calcular nosso vetor normal.
Mas repara que esse plano é paralelo ao . O vetor normal a todo o é o vetor , que é o sentido do eixo , certo? Então ele também vai ser normal ao nosso plano!
Repara que a componente do nosso vetor é sempre positiva, então ele está virado para cima como queremos.
Passo 8
Com isso, a gente consegue montar a integral:
Vimos que
A integra fica:
Passo 9
Calculando esse produto escalar,
Ih olha só, se essa integral zera, então:
Usar outra superfície ajudou tanto que a gente nem precisou calcular a integral da forma completona. Legal, né?
Resposta
a) 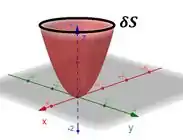
b)