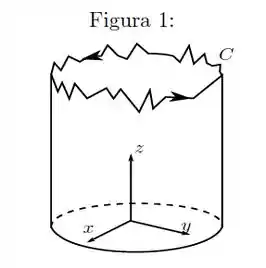
Considere um vidro cilíndrico quebrado sobre o plano de maneira que sua base se encontra no círculo com a curva de classe por partes e orientada no sentido anti-horário como na Figura . Dado o campo vetorial
Calcule .
Passo 1
Esses professores viajam, né? Começa a falar de vidro quebrado, que sei lá o que, pra no final pedir uma integral de linha, nada a ver... Mas a gente não pode fazer nada, vamos ver como que dá pra resolver essa questão.
A gente não tem a parametrização da curva e, como essa figura maluca aí, nem dá pra obtermos. Então não tem jeito, vamos ter que pensar num Stokes aí. O teorema diz que:
Mas como que vamos encontrar uma superfície que use como fronteira se nem sabemos como é a curva direto?
Aí que ta o macete! Vamos usar esse cilindro aí da figura (sim, a historinha toda do vidro quebrado era só pra isso).
A única coisa que temos que ficar ligados é que o cilindro tem uma fronteira em cima, a curva estranha, e outra embaixo, a sua base, que no enunciado ele diz que é o círculo , e que vamos chamar de porque ela deve ter orientação no sentido horário, já que está no sentido anti-horário.
Então na verdade vamos ter:
Vamos ver se conseguimos calcular agora!
Passo 2
Vamos começar com o fluxo do rotacional, que pode ser calculado assim:
O que podia ser melhor, se fosse nem precisariamos calcular a integral. Mas como não é, vamos usar a fórmula:
Então vamos parametrizar a superfície. Temos um cilindro de raio , a parametrização fica, simplesmente:
E o normal:
Agora, a gente vai ter que .
Repara agora que nem precisamos verificar se nosso vetor normal está na sentido certo, porque independente do sentido a integral vai dar zero! Se liga:
E por dar não precisamos nem ver o domínio também!
Passo 3
Agora vamos ver a integral de linha da base lá. Vamos usar a fórmula:
é uma circunferência no plano , então vamos parametrizar assim:
O vetor tangente fica:
E a integral:
E se lembrarmos que :
Passo 4
Agora é só somar, como vimos na relação lá em cima:
E pronto, achamos o que ele pediu!