Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 811234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 3, lista 3 - 2021.1, Questão 12a

( a ) Calcule ∫ γ ( z + y 2 ) d x + ( y 2 + 1 ) d y + [ l n ( z 2 + 1 ) + y ] d z , sendo γ ( t ) = ( 2   c o s ( t ) ,   2   s e n ( t )   , 10   - 2   s e n ( t ) ) ,   t   ∈ [ 0,2 π ] .

Passo 1

Eaew, belezinha?

O enunciado é bastante direto desta vez, pedindo para calcularmos a seguinte integração

∫ γ ( z + y 2 ) d x + ( y 2 + 1 ) d y + [ l n ( z 2 + 1 ) + y ] d z

que é uma integral de linha ao longo da curva

γ ( t ) = ( 2   c o s ( t ) ,   2   s e n ( t )   , 10   - 2   s e n ( t ) ) ,   t   ∈ [ 0,2 π ]

para isso, vamos utilizar o teorema de Stokes que faz a seguinte identificação

∫ γ F → ⋅ d r → = ∫ ∫ S r o t ( F → ) ⋅ n →   d S

em que

F → = [ z + y 2 , y 2 + 1 , l n ( z 2 + 1 ) + y ]

Consegue ler a definição acima? Se não, vem comigo!

Passo 2

Vamos calcular as grandezas no lado direito do teorema de Stokes! Podemos começar com

r o t ( F → ) = ∇ → × F →

usando que ∇ → = ( ∂ ∂ x , ∂ ∂ y , ∂ ∂ x ) , e usando a fórmula para o produto vetorial, temos

r o t ( F → ) = ( ∂ F z ∂ y - ∂ F y ∂ z , ∂ F x ∂ z - ∂ F z ∂ x , ∂ F y ∂ x - ∂ F x ∂ y )

precisamos calcular todas as derivadas parciais! Vamos fazer uma de cada vez

∂ F z ∂ y = ∂ ∂ y [ l n ( z 2 + 1 ) + y ]

como temos a derivada parcial em y , tudo que não depende de y é uma constante, temos então que

∂ F z ∂ y = 0 + 1 = 1

já que o termo de logaritmo não depende de y . Analogamente, vamos calcular as outras derivadas parciais

∂ F y ∂ z = ∂ ∂ z [ y 2 + 1 ] = 0

∂ F x ∂ z = ∂ ∂ z [ z + y 2 ] = 1

∂ F z ∂ x = ∂ ∂ x [ l n ( z 2 + 1 ) + y ] = 0

∂ F y ∂ x = ∂ ∂ x [ y 2 + 1 ] = 0

∂ F x ∂ y = ∂ ∂ y [ z + y 2 ] = 2 y

Maravilha! As derivadas acima são todas que precisávamos! Substituindo no rotacional, temos que

r o t ( F → ) = ( 1 - 0,1 - 0,0 - 2 y ) = ( 1,1 , 2 y )

Ótimo! O rotacional ficou razoavelmente simples! Agora, precisamos do nosso vetor normal! Vamos lá!

Passo 3

A expressão do vetor normal pode ser obtida através do seguinte produto vetorial

n → = ∂ ϕ ( u , v ) ∂ u × ∂ ϕ ( u , v ) ∂ v

em que ϕ ( u , v ) é uma parametrização da superfície que tem como fronteira a curva dada por

γ ( t ) = ( 2   c o s ( t ) ,   2   s e n ( t )   , 10   - 2   s e n ( t ) ) ,   t   ∈ [ 0,2 π ]

Note que nas variáveis x ( t ) e y ( t ) temos uma circunferência, portanto, vamos escolher a parametrização de nossa superfície usando coordenadas polares

ϕ ( r , θ ) = ( r   c o s ( θ ) , r   s e n ( θ ) , 10 - r   s e n ( θ ) )

em que temos 0 ≤ r ≤ 2 e 0 ≤ θ ≤ 2 π . O vetor normal pode ser escrito como

n → = ∂ ϕ ( r , θ ) ∂ r × ∂ ϕ ( r , θ ) ∂ θ

Vamos calcular as derivadas e o produto vetorial!

Passo 4

Usando a parametrização e calculando a derivada em relação a r , temos que

∂ ϕ ( r , θ ) ∂ r = ∂ ∂ r [ ( r   c o s ( θ ) , r   s e n ( θ ) , 10 - r   s e n ( θ ) ) ] = ( c o s ( θ ) , s e n ( θ ) , - s e n ( θ ) )

agora para a derivada em relação a θ temos que

∂ ϕ ( r , θ ) ∂ θ = ∂ ∂ θ [ ( r   c o s ( θ ) , r   s e n ( θ ) , 10 - r   s e n ( θ ) ) ] = ( - r s e n ( θ ) , r   c o s ( θ ) , - r   c o s ( θ ) )

Aplicando a definição de produto vetorial temos que

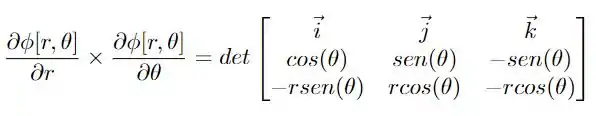
aplicando o determinante, temos então que

n → = ( - r   s e n ( θ ) c o s ( θ ) + r s e n ( θ ) c o s ( θ ) , r   s e n 2 ( θ ) + r c o s 2 ( θ ) , r   c o s 2 ( θ ) + r   s e n 2 ( θ ) )

usando a identidade trigonométrica c o s 2 ( θ ) + s e n 2 ( θ ) = 1 , obtemos que

n → = ( 0 , r   , r )

Agora, vamos voltar para a nossa integral!

Passo 5

A integral é tal que

∫ γ F → ⋅ d r → = ∫ ∫ S r o t ( F → ) ⋅ n →   d S

como escolhemos coordenadas polares para parametrizar a nossa superfície, temos que d S = d r d θ , portanto

∫ γ F → ⋅ d r → = ∫ 0 2 π ∫ 0 2 ( 1,1 , 2 y ) ⋅ ( 0 , r , r )   d r   d θ

mas ainda temos ali um y que está incomodando, em nossas coordenadas, temos que y ( r , θ ) = r   s e n ( θ ) , portanto, temos

∫ γ F → ⋅ d r → = ∫ 0 2 π ∫ 0 2 ( 1,1 , 2 r   s e n ( θ ) ) ⋅ ( 0 , r , r )   d r   d θ

calculando o produto escalar, temos que

∫ γ F → ⋅ d r → = ∫ 0 2 π ∫ 0 2 [ ( 1 ) ( 0 ) + ( 1 ) ( r ) + ( 2 r   s e n ( θ ) ) ( r ) ]   d r   d θ = ∫ 0 2 π ∫ 0 2 [ r + 2 r 2 s e n ( θ ) ] d r d θ

Vamos fazer a integral em θ e r separadamente já que os limites aqui são constantes! Saca só!

Passo 6

Temos a integral em θ dada por

∫ 0 2 π ∫ 0 2 [ r + 2 r 2 s e n ( θ ) ] d r d θ = ∫ 0 2 r [ ∫ 0 2 π d θ ] d r + 2 ∫ 0 2 r 2 [ ∫ 0 2 π s e n ( θ ) d θ ] d r

usando que

∫ 0 2 π d θ = θ | 0 2 π = 2 π

e, que

∫ 0 2 π s e n ( θ ) = - c o s ( θ ) | 0 2 π = 0

Obtemos simplesmente que

∫ 0 2 r [ ∫ 0 2 π d θ ] d r + 2 ∫ 0 2 r 2 [ ∫ 0 2 π s e n ( θ ) d θ ] d r = 2 π ∫ 0 2 r d r

Maravilha! Agora vamos resolver a integral em r !

Passo 7

Temos a seguinte integração

∫ 0 2 r d r

usando a regrinha para integração de polinômios, temos que

∫ 0 2 r d r = 1 1 + 1 r 1 + 1 | 0 2 = 1 2 r 2 | 0 2

Avaliando os limites de integração

∫ 0 2 r d r = 2 2 2 - 0 2 2 = 2

Juntando os dois resultados obtidos, temos que o nosso resultado final é

∫ 0 2 π ∫ 0 2 [ r + 2 r 2 s e n ( θ ) ] d r d θ = 2 π ( 2 ) = 4 π

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

∫ γ ( z + y 2 ) d x + ( y 2 + 1 ) d y + [ l n ( z 2 + 1 ) + y ] d z = 4 π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê