Calcule sendo:
e formada pelas faces, que não estão no plano , do tetraedro formado pelos planos coordenadas e o plano , sendo o campo normal exterior ao tetraedro.
Passo 1
Eaew, belezinha?
Precisamos calcular a integral de superfície
em que o campo vetorial é dado por
O campo vetorial é relativamente simples, e temos que parametrizar uma curva que seja fronteira da região indicada será complicado! Portanto, vamos usar a definição de integral de fluxo para calcular a integral desejada! Saca só!
Passo 2
Temos que o nosso tetraedro é o seguinte
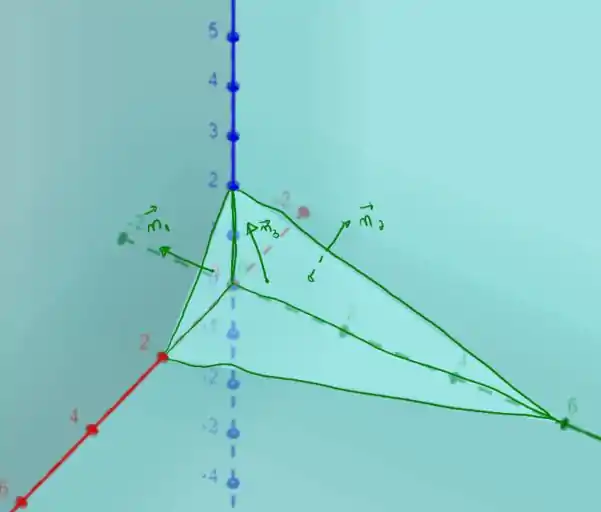
como temos três faces a se considerar, eu as indiquei com os vetores normais , e . A integral de superfície deve ser considerada individualmente para cada uma dessas faces, portanto, iremos ter que calcular
Normalmente esse seria um trabalho bastante penoso! Mas nossos vetores normais são facilmente identificáveis! Saca só!
Passo 3
Temos que as faces e são os planos e . Olhando a figura que apresentei é bastante simples identificar que suas componentes são
e
Para o vetor normal que falta podemos usar a equação geral do plano dada
da qual podemos identificar que o vetor normal ao plano é simplesmente
Todos eles apontam para fora da superfície! Portanto, são adequados para o que queremos fazer! Vamos calcular agora o rotacional do campo vetorial!
Passo 4
Temos que o rotacional pode ser calculado usando a definição
calculando as derivadas parciais, temos que
Finalmente podemos escrever as nossas integrações como
da mesma forma, temos que
e, por último, temos que
Vamos resolver cada uma delas individualmente!
Passo 5
Vamos começar com a mais difícil, enquanto ainda temos forças, temos que
Podemos expandir o produto escalar para obter
para conseguir determinar os limites de integração, vamos notar que temos a seguinte situação
em que está no intervalo , mas se seguirmos inicialmente ao longo de , note que ao avançar por , encontraremos a seguinte reta
obtida com a interseção em em nosso plano. Os limites são então dados por . E, a nossa integral se torna
Vamos expandir e resolver agora! Saca só!
Passo 6
Integrando primeiro em já que os limites não são constantes, ainda bem que todos os termos são polinômios, portanto, podemos integrá-los facilmente para obter
avaliando os limites de integração temos que
Vamos expandir um pouco os produtos apenas para ficar mais fácil visualizar os polinômios, temos que
Integrando temos então que
Vamos para as outras duas agora!
Passo 7
Vamos trabalhar agora com
expandindo o produto escalar
no entanto, esta superfície é o plano tal que , e portanto, temos simplesmente que
esta superfície é o plano no qual , e a superfície está no plano . Note que temos que podemos considerar no intervalo , mas isso acarreta em considerarmos que estará no intervalo
Portanto a integral toma a forma
Precisamos integrar primeiro em , de forma que obtemos
Integrando agora em , temos que
Vamos analisar a outra integral agora!
Passo 8
Temos restando apenas a integral
expandindo o produto escalar
esta superfície é o plano no qual , e a superfície está no plano . Portanto, podemos garantir que
Juntando todos os resultados que obtivemos, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!