34) Calcule
Sendo um campo em dado por
Onde é de classe , tal que em e é a intersecção da superfície com o plano , com uma orientação tal que quando projetada no plano produz um percurso no sentido horário.
Passo 1
Caraca, tem muitas informações nesse enunciado (gradiente e vários outros) então vamos começar filtrando essas informações a partir do que a gente quer: a resolução da integral de linha!
Uma integral de linha sempre podemos pensar em pelo menos duas formas de se resolver:
1º - De uma forma direta.
2º - Utilizando o Teorema de Stokes.
Ora! Não temos informações muito precisas sobre o campo (ele depende de um outro cara que pouco sabemos, o ). Isso é um ótimo indício de que o Teorema de Stokes vai nos ajudar aqui.
Se você tá preocupado com aquele produto escalar do gradiente ali, calma! Já já você vai entender onde ele vai entrar na brincadeira. Vamos continuar de forma normal a resolução 😉
Passo 2
Tão tá bom sabemos que Stokes pode resolver o problema, mas o que ele fala mesmo? Bem basicamente ele iguala a integral de linha com uma de superfície dessa forma aqui:
Assim, ao invés de termos que calcular uma integral de linha, podemos calcular uma integral de superfície que pode facilitar, saca?
Porém Stokes não é só isso! Para aplicar a igualdade entre as integrais antes devemos averiguar as condições desse Teorema, que nos pede basicamente três coisas:
1º - Uma curva fechada delimitando uma superfície .
2º - Sem singularidades na função Vetorial.
3º - Superfície orientada positivamente.
Vamos passar por cada um deles e verificar se satisfazem ou não 😊!
Passo 3
A curva dada no problema é a curva que está dada na intersecção de outras duas superfícies:
1º - Um cilindro de raio ():
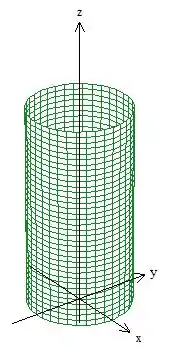
2º - Um plano paralelo ao eixo :
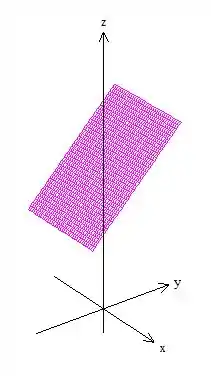
Juntando essas duas coisas, olha quem encontramos:
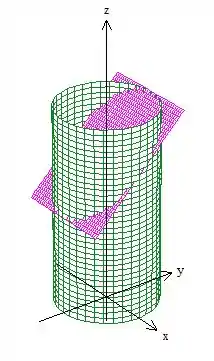
Exatamente! Uma curva que é fechada e delimita um disquinho: uma superfície fechada que daremos um nome de .
Passo 4
A outra condição é:
2º - Sem singularidades na função Vetorial.
Ora, sim! Basta ver o campo
Para você perceber que o campo não tem nenhum bug ou singularidade, como uma divisão por em algum ponto ou algo assim.
Embora não conhecemos bem , sabemos que ele é de classe e isso já é o suficiente pra dizer que ele também não buga em nenhuma parte do espaço (Pois ele é contínuo).
Passo 5
3º - Superfície orientada positivamente.
Aqui o que temos que fazer é garantir que o conjunto curva-superfície esteja orientadas positivamente. Pow, pelo enunciado, a projeção da curva no gira no sentido horário. Então a curva no espaço também gira:
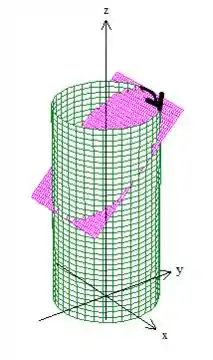
Pela regra da mão direita temos que ter um vetor normal pra baixo na superfície circular. Agora elas estão sim orientadas positivamente, saca?
Passo 6
Com as condições averiguadas e sendo satisfeitas, podemos aplicar a igualdade numa nice:
Onde a gente pode encontrar esse rotacional numa boa fazendo...
Como
Então derivando lembrando que, e , ...
Hey! A gente vai ficar com o rotacional assim? É melhor a gente ver agora o que significa aquele produto escalar do gradiente, pois não sei se você se lembra, mas gradiente nos dá informação sobro derivadas parciais! Bem, pelo enunciado:
O gradiente é o vetor de derivadas parciais
Fazendo esse produto escalar com o ...
Então o rotacional fica...
Se o problema não nos deu a informação sobre , é porquê provavelmente não vamos precisar, ok, então bora continuar o problema!
Para calcular a integral de superfície e fugir da integral de linha, precisamos:
1º - Parametrizar a superfície .
2º - Encontrar o termo .
Passo 7
Para parametrizar a superfície saca só: estamos em cima de um plano...
Então podemos parametrizar de forma explícita, pois o é um cara livre (parâmetro) e depende de que também é um cara livre...
Agora esses parâmetros estão variando dentro do cilindro que é quem delimita o plano formando o disquinho elíptico:
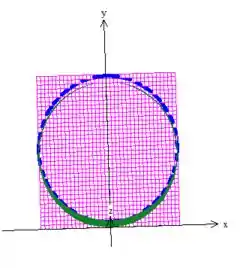
Então a gente pode falar que, vendo de cima pra baixo, o e o estão variando no círculo de raio devido a equação do cilindro ().
Por hora, vamos apenas falar que o e o estão variando dentro da região circular
Passo 8
Para o termo , que é a nossa segunda tarefa na resolução da integral de superfície...
Onde o é fácil de se obter pelo macete de parametrização por gráfico de função ...
Ahhhh! Veja que esse vetor normal não atende lá as condições de termos o vetor normal pra baixo. Se não atende é só inverter o sinal...
Então...
Passo 9
Jogando esses dados então na integral de superfície...
Calculando o produto escalar...
Poxa, a integral de é a área de ...
Como o raio desse círculo é ...
Pelo teorema de Stokes...