Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 451234567891011121314151617181920212223242526272829303132333435363738394041424344464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 3:

Seja

F → x ,   y ,   z = x 7 ,   z + e y 2 , cos ⁡ z 2 + x y

e γ a intersecção do cilindro x 2 16 + y 2 9 = 1 com o paraboloide z = x 2 + y 2 - 1 orientada de forma que sua projeção no plano x y seja percorrida uma vez no sentido horário. Calcule ∫ γ   F → ⋅ d r → .

Passo 1

Bem, queremos calcular uma integral de linha em cima de uma curva γ no espaço dado pela intersecção de um cilindro com uma paraboloide. O cilindro está com uma base elíptica, mas esse detalhe não é tão relevante agora. Desenhando no espaço...

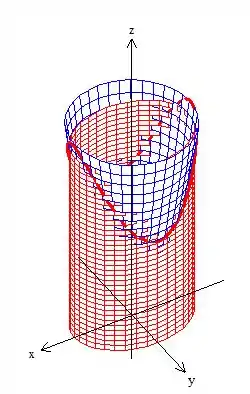
Ou melhor, a curva de intersecção é essa daqui vermelhona:

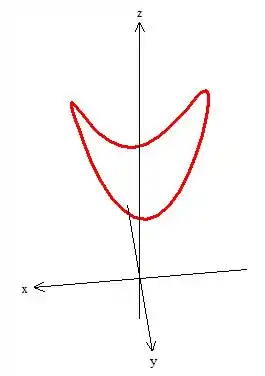
Calcular uma integral de linha em cima dessa curva estranha de uma forma direta não vai ser legal, por isso, podemos pensar no método alternativo: o Teorema de Stokes. Se quiser ter mais provas de que de fato estamos lidando com esse teorema, calculemos o rotacional !

Passo 2

O rotacional de um campo F → pode ser dado fazendo

r o t F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z , ∂ F 1 ∂ z - ∂ F 3 ∂ x , ∂ F 2 ∂ x - ∂ F 1 ∂ y

Como no nosso caso...

F → x ,   y ,   z = x 7 ⏟ F 1 ,   z + e y 2 ⏟ F 2 , cos ⁡ z 2 + x y ⏟ F 3

Calculando essas derivadas parciais encontramos:

r o t F → = x - 1 ,   0 - y , 0 - 0

r o t F → = x - 1 ,   - y , 0

Poxa, um rotacional simples assim só pode nos indicar para realmente usarmos Stokes que nos esta igualdade:

∫ γ   F → ⋅ d r → = ∬ S   r o t F → ⋅ n →   d S

Mas cuidado! Não podemos sair aplicando essa igualdade de qualquer forma. Precisamos antes averiguar as condições do Teorema.

Passo 3

O teorema de Stokes nos pede três coisas antes de aplicarmos a sua igualdade:

1 º - Precisamos de uma curva fechada delimitando uma superfície S .

Ora, a nossa curva já é fechada, e a superfície que ela delimita, podemos pegar o interior do próprio paraboloide

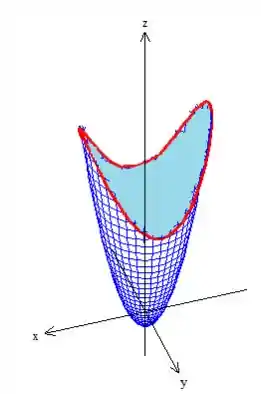
2 º - Outra exigência do teorema é que o campo F → x ,   y ,   z , não tenha singularidades onde estamos trabalhando. O que já é satisfeito pelo fato do campo não ter nenhum bug como uma divisão por zero ou algo assim:

F → x ,   y ,   z = x 7 ,   z + e y 2 , cos ⁡ z 2 + x y

3 º - A última, nos fala que a curva e a superfície devem estar orientadas positivamente. Vamos analisar isso com mais calma.

Passo 4

O problema nos disse que se olhássemos de cima para baixo na curva, os veríamos girando no sentido anti-horário:

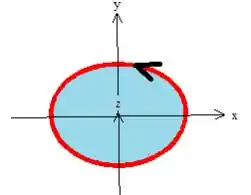
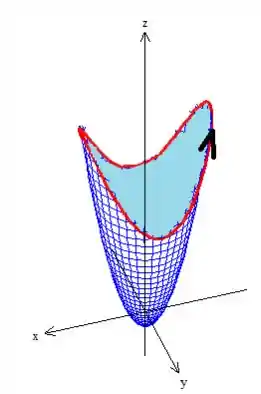
A superfície que escolhemos, no caso o paraboloide, também deve estar orientado de forma que satisfaça esse giro da curva. Para isso, usamos a regra da mão direita, onde os dedos estão na direção de giro dela enquanto que o polegar mostra o sentido do vetor normal

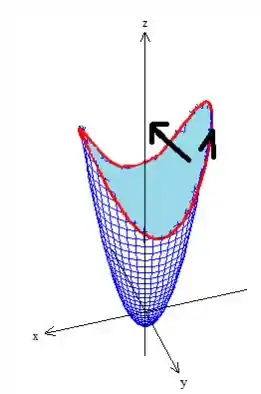
O que no caso está pra cima com a coordenada z positiva ;)

Passo 5

Beleza, então as condições do Teorema sendo satisfeitas, podemos aplicar a igualdade de Stokes:

∫ γ   F → ⋅ d r → = ∬ S   r o t F → ⋅ n →   d S

Se queremos calcular a integral de linha, basta calcular a de superfície e encontramos o resultado, saca?

A integral de superfície, não tem por onde correr... Deve ser feita do modo diretão:

1º - Parametrizando a superfície S .

2º - Substituindo os termos da parametrização no rotacional de F → .

3º - Calculando o termo n →   d S .

Passo 6

No caso da parametrização, como a superfície que escolhemos foi um paraboloide com equação explícita

z = x 2 + y 2 - 1

Podemos pensar em uma parametrização também explícita, onde os parâmetros são o próprio x e y

σ x ,   y = x ,   y ,   x 2 + y 2 - 1

Olhando para a superfície de cima para baixo

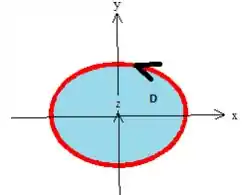
Notamos que estamos trabalhando dentro desse círculo limitado pelo cilindro x 2 16 + y 2 9 = 1 . Por hora, podemos falar apenas que x e y estão variando em D

x , y ∈ D

Passo 7

Deveríamos agora trocar os termos da função rotacional

r o t F → = x - 1 ,   - y , 0

Pelos termos da parametrização. Porém, se você reparar, o x e o y não mudou, ou seja, continuaram a ser x e y . O único que mudou, foi o z , mas o rotacional no caso não depende de z , então ele permanece o mesmo, saca?

r o t F → = x - 1 ,   - y , 0

Passo 8

Calculemos agora o termo n →   d S ...

n →   d S = N →   d x d y

Como parametrizamos na forma de gráfico de uma função explícita...

z x ,   y = x 2 + y 2 - 1

Podemos usar o bizu do vetor normal, para agilizarmos o processo...

N → = - d z d x ,   - d z d y , �� 1 →

N → = - 2 x ,   - 2 y ,   1

Repare que esse vetor norma, atende a condição que vimos, ou seja, apontado pra cima, afinal o termo que corresponde ao z é 1 e é positivo ;)

Potanto:

n → d S = - 2 x ,   - 2 y ,   1

Passo 9

Retornando ao problema que faremos por S t o k e s

∫ γ   F → ⋅ d r → = ∬ S   r o t F → ⋅ n →   d S

E substituindo os termos na integral de superfície, ganhamos a integral dupla...

∬ D   x - 1 ,   - y , 0 ⋅ - 2 x ,   - 2 y ,   1 d x d y =

∬ D   - 2 x 2 + 2 x + 2 y 2 d x d y

Como D é uma região elíptica...

podemos usar as mudanças para coordenadas elípticas

x 2 4 2 + y 2 3 2 = 1

x = 4   r cos ⁡ θ

y = 3   r sin ⁡ θ

Não se esqueça que o Jacobiano no caso é

J = 4 ⋅ 3 ⋅ r = 12 r

O r varia de 0 a 1 , pois quando r = 1 , tem a elipse vermelha da borda máxima. Enquanto que o θ dá uma volta completa...

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

Logo...

∬ D   - 2 x 2 + 2 x + 2 y 2 d x d y = ∫ 0 2 π ∫ 0 1 - 2 4   r cos ⁡ θ 2 + 2 4   r cos ⁡ θ + 2 3   r sin ⁡ θ 2 ⋅ 12 r   d r d θ =

Podemos simplificar um pouco essa expressão...

12 ∫ 0 2 π ∫ 0 1 - 32 r 2 cos 2 ⁡ θ + 8   r cos ⁡ θ + 18   r 2 sin 2 ⁡ θ ⋅ r   d r d θ =

12 ∫ 0 2 π ∫ 0 1 - 32 r 3 cos 2 ⁡ θ + 8   r 2 cos ⁡ θ + 18   r 3 sin 2 ⁡ θ   d r d θ =

12 ∫ 0 2 π ∫ 0 1 r 3 - 32 cos 2 ⁡ θ + 18 sin 2 ⁡ θ + 8   r 2 cos ⁡ θ   d r d θ =

E agora calcular uma integral em r (considerando então a expressão com θ constante):

12 ∫ 0 2 π ∫ 0 1 r 3 - 32 cos 2 ⁡ θ + 18 sin 2 ⁡ θ + 8   r 2 cos ⁡ θ   d r d θ =

12 ∫ 0 2 π r 4 4 0 1 - 32 cos 2 ⁡ θ + 18 sin 2 ⁡ θ + r 3 3 0 1 8 cos ⁡ θ d θ =

Substituindo os limites de integração de r d simplificando mais um pouco chegamos à...

12 ∫ 0 2 π 1 4 - 32 cos 2 ⁡ θ + 18 sin 2 ⁡ θ + 8 3 cos ⁡ θ d θ =

12 ∫ 0 2 π - 8 cos 2 ⁡ θ + 9 2 sin 2 ⁡ θ + 8 3 cos ⁡ θ d θ

Agora aqui, lembre-se de que podemos trocar esses senos e cossenos ao quadrado por duas expressões maaaaras da trigonometria:

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2   e   sin 2 ⁡ θ = 1 - cos ⁡ 2 θ 2

Onde vamos ficar com...

12 ∫ 0 2 π - 8 1 2 + cos ⁡ 2 θ 2 + 9 2 1 2 - cos ⁡ 2 θ 2 + 8 3 cos ⁡ θ d θ =

12 ∫ 0 2 π - 4 - 4 cos ⁡ 2 θ + 9 4 - 9 cos ⁡ 2 θ 8 + 8 3 cos ⁡ θ d θ =

Colocando em evidência o cosseno e integrando, obtemos...

12 ∫ 0 2 π - 7 4 - 41 8 cos ⁡ 2 θ + 8 3 cos ⁡ θ d θ =

12 - 7 4 θ - 41 8 ⋅ sin ⁡ 2 θ 2 + 8 3 sin ⁡ θ 0 2 π =

12 - 7 π 2 = - 42 π

Logo, pelo Teorema de Stokes...

∫ γ   F → ⋅ d r → = - 42 π

Resposta

- 42 π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê