USP, Sem Campus, Cálculo 3, lista 3 - 2021.1, Questão 18a
Calcule sendo:
e a parte do parabolóide que está acima do plano , orientada pelo campo de vetores normais que aponta para cima;
Passo 1
Eaew, belezinha?
Precisamos calcular a integral de superfície
em que o campo vetorial é dado por
O fato de que ele está pedindo exatamente o lado direito do teorema de Stokes me faz questionar que talvez eu deva usá-lo! Portanto, vamos tentar aplicar a seguinte identificação
em que é uma curva fronteira à nossa superfície ! Se conseguirmos encontrar essa curva e o formato for bem simples, podemos expandir o lado direito através de uma parametrização! Bora lá!
Passo 2
Vamos tentar encontrar a curva, nós temos a seguinte região
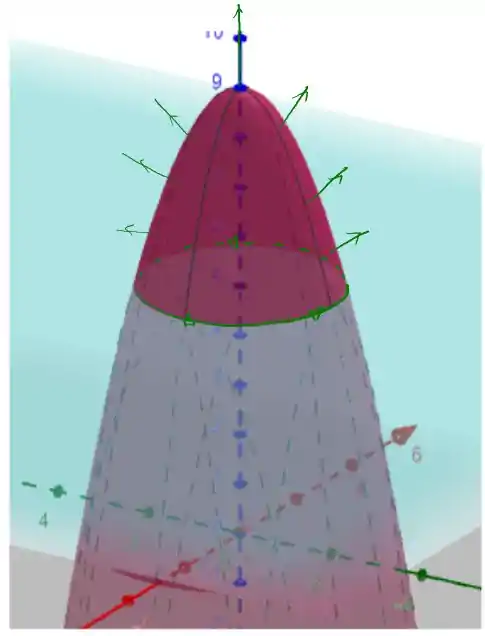
Note que a curva é a interseção do parabolóide dado com o plano , obtemos que
ou seja, podemos identificar a seguinte circunferência
Ou seja, é uma curva bastante simples de se parametrizar! Vamos seguir com o problema!
Passo 3
A integral de linha do lado esquerdo do teorema de Stokes pode ser expandida da seguinte maneira
Como obtivemos que a nossa curva é uma circunferência de raio , vamos parametrizá-la da seguinte maneira
se derivarmos em relação ao parâmetro, temos que
Maravilha! Com isso em mãos vamos aplicar em nossa integração!
Passo 4
Primeiro, vamos usar a parametrização em nosso campo vetorial para obter
Portanto, calculando o escalar do campo acima com a derivada da parametrização da curva, temos que
Desta forma precisamos resolver a seguinte integração
Vamos tratar de resolver elas agora!
Passo 5
Primeiro, temos que podemos identificar diretamente o resultado
e, usando a relação de meio ângulo para o seno, podemos escrever a outra integral como
Usando que
e que
Obtemos finalmente que
ou seja, o teorema de Stokes nos garante que
A questão foi isso! Te vejo na próxima! Tchau Tchau!