Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 461234567891011121314151617181920212223242526272829303132333435363738394041424344454748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 2) Considere o campo vetorial F → x ,   y ,   z = x j → + x y k → e S a superfície descrita pelas relações x 2 + y 2 + z 2 4 = 1 e z ≤ 1 , orientada de modo que o vetor normal no ponto 0 ,   0 ,   - 2 esteja apontando para baixo.

  1. Parametrizar positivamente a curva fronteira de S .
  2. Calcule o fluxo do rotacional de F → através de S .

Passo 1

a )

Para vermos a curva fronteira e ter uma noção de quem ela é, desenhemos a superfície S indicada no problema: sabemos que S é o elipsoide x 2 + y 2 + z 2 4 = 1

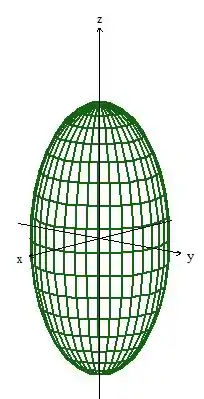
Mas cortado pelo plano z = 1 ...

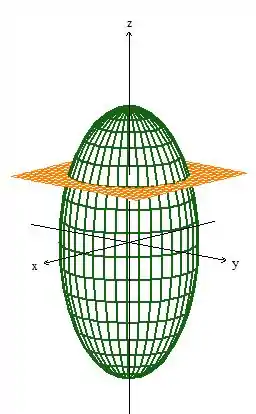
E eis que aparece o S ali em baixo já que z ≤ 1 ...

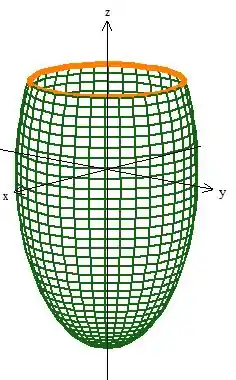
Veja então que a curva fronteira de S é aquela circunferência ali, e ela é obtida na intercessão do plano com o elipsoide:

x 2 + y 2 + z 2 4 = 1   z = 1         →

x 2 + y 2 + 1 4 = 1       →           x 2 + y 2 = 4 4 - 1 4               →

x 2 + y 2 = 3 4

No caso é uma circunferência de raio 3 2 ;D

Passo 2

Então temos que parametrizar uma circunferência. Ora, basta a gente então parametrizar com a parametrização polar...

x = R cos ⁡ θ

y = R sin ⁡ θ

z = 1

Onde R não é parâmetro, afinal como é uma curva só tem um parâmetro ( θ ). R é o raio da circunferência que no caso R = 3 2 ... Logo a parametrização final dessa borda é...

r → θ = 3 2 cos ⁡ θ ,   3 2 sin ⁡ θ ,   1

Onde θ tem que dar uma volta completa ao redor do z , lodo...

0 ≤ θ ≤ 2 π

Passo 3

Embora já encontramos uma parametrização, se você perceber essa curva gira no sentido anti-horário vista de cima, já que θ é o cara que gira a partir do eixo x ...

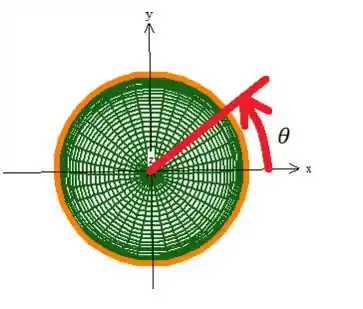
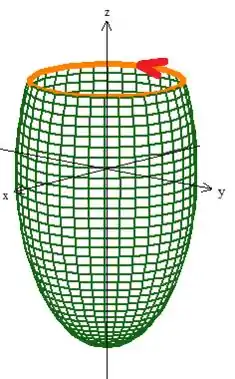
Qual é o problema disso? É que o problema pediu para que arrumássemos uma curva orientada positivamente, ou seja, que gire de acordo com o vetor normal. O problema nos disse que o vetor normal é um cara que no ponto 0 ,   0 ,   - 2 ele aponta pra baixo...

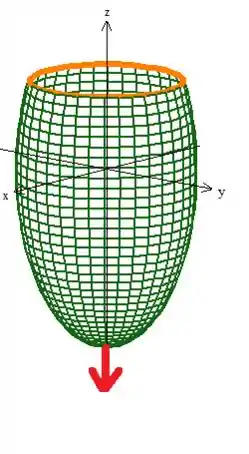
Então pela regra da mão direita, a borda deveria estar girando no sentido horário (contrário do que está na real):

Então para corrigir esse detalhe, basta pegarmos a parametrização que encontramos...

r → θ = 3 2 cos ⁡ θ ,   3 2 sin ⁡ θ ,   1       →

E trocarmos as duas primeiras coordenadas...

r → θ = 3 2 sin ⁡ θ ,   3 2 cos ⁡ θ ,   1       c o m         θ ∈ 0 ,   2 π

Agora a curva gira no sentido positivo, ou seja, no sentido horário como manda o vetor normal:

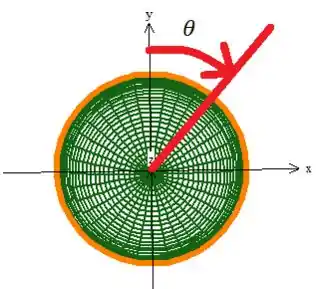
Passo 4

b )

O fluxo de um rotacional de um campo através de uma superfície S é dado por uma integral de superfície

∬ S   r o t F → ⋅ n →   d S

Como já temos uma curva C parametrizada, isso já é um indício de que iremos ter que utilizar o Teorema de Stokes, pois esse teorema relaciona

∫ C   F → ⋅ d r → = ∬ S   r o t F → ⋅ n →   d S

Onde C tem que ser uma curva fechada e borda de S (o que acontece). Ahhh, e C também tem que estar orientada positivamente (o que acabamos de fazer ). Sendo assim, podemos trocar o trabalho de calcular a integral de superfície pelo trabalho de calcular a integral de linha. Vem comigo!

Passo 5

∫ C   F → ⋅ d r →

A curva C já está parametrizada positivamente...

r → θ = 3 2 sin ⁡ θ ,   3 2 cos ⁡ θ ,   1       c o m         θ ∈ 0 ,   2 π

Para o termo d r → , basta derivar em relação a θ ...

d r → = 3 2 cos ⁡ θ , -   3 2 sin ⁡ θ ,   0 d θ

O campo F → = 0 ,   x ,   x y tem que ser transformado nas novas coordenadas (basta observar a parametrização)...

F → = 0 ,   x ,   x y = 0 ,   3 2 sin ⁡ θ ,   3 4 sin ⁡ θ cos ⁡ θ

Voltando para a integral de linha...

∫ C   F → ⋅ d r → = ∫ 0 2 π 0 ,   3 2 sin ⁡ θ ,   3 4 sin ⁡ θ cos ⁡ θ ⋅ 3 2 cos ⁡ θ , -   3 2 sin ⁡ θ ,   0 d θ =

Calculando o produto escalar:

∫ C   F → ⋅ d r → = - 3 4 ∫ 0 2 π sin 2 ⁡ θ d θ

Agora é só resolver essa integral e correr para o abraço.

Passo 6

- 3 4 ∫ 0 2 π sin 2 ⁡ θ d θ =

Lembrando que sin 2 ⁡ θ = 1 - cos ⁡ 2 θ 2 ...

- 3 4 ∫ 0 2 π sin 2 ⁡ θ d θ = - 3 4 ∫ 0 2 π 1 2 - cos ⁡ 2 θ 2 d θ =

- 3 4 1 2 θ - sin ⁡ 2 θ 4 0 2 π =

- 3 4 1 2 2 π - sin ⁡ 4 π 4 - 1 2 0 - sin ⁡ 0 4 =

- 3 4 π - 0 - 0 - 0 = - 3 π 4

Logo, pelo teorema de Stokes o fluxo do rotacional em S ...

∬ S   r o t F → ⋅ n →   d S = - 3 π 4

Resposta

a)

r → θ = 3 2 sin ⁡ θ ,   3 2 cos ⁡ θ ,   1       c o m         θ ∈ 0 ,   2 π

b)

- 3 π 4

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê