Exercícios Resolvidos de Teorema de Stokes

Ver Teoria

Exercício 88 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

Teorema de Stokes

Use o teorema de Stokes para calcular a integral de linha , em que

Em que é a curva de intersecção do plano com o cilindro .

Passo 1

Antes de tudo vamos fazer um gráfico da região para entender melhor a questão. Temos o plano cortado pelo cilindro de raio centrado na origem, o que nos dá isso aqui:

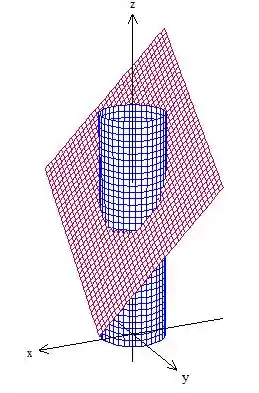
Esse desenho não precisa de precisão nenhuma, ok? É só para termos uma ideia mesmo, você pode desenhar um plano qualquer cortando o clilindro.

A questão pede para calcularmos a integral de linha em , que é a interseção do plano inclinado (em vermelho) com o cilindro. Como podemos ver, forma uma elipse. Percebeu?

Passo 2

O Teorema de Stokes nos diz isso aqui:

Ou seja, podemos substituir essa integral de linha sobre a curva por uma integral do rotacional de sobre uma superfície que tenha a curva como fronteira. No caso, vamos escolher esse retalho do plano mesmo, para simplificar as coisas! Ou seja, a própria elipse contida no plano.

Então, é o pedaço do plano que forma uma elipse inclinada e é a própria curva , a fronteira do plano.Temos então:

Precisamos, então, calcular , sabendo que

Temos:

Passo 3

Agora vamos parametrizar a superfície .

Há infinitas superfícies com fronteira igual à curva do enunciado, mas para simplificar o problema, escolhemos o retalho do plano mesmo.

Qual será a melhor maneira para parametrizar o plano? Vamos usar logo e como parâmetros, para ser mais simples:

Onde e pertencem à projeção dessa região no plano , que, no caso, é um círculo. Como assim? Vendo de cima, temos isso aqui:

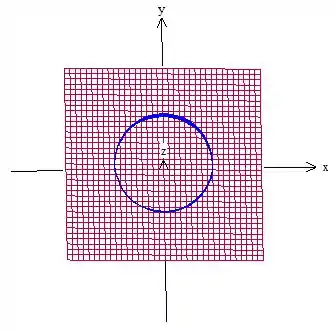
A elipse inclinada “vira” um círculo, a projeção do cilindro. Então, e tem que estar dentro dessa circunferência azul, de equação

Foi? Isso acontece porque o plano é cortado pelo cilindro. Temos então

Com

Esse é o domínio da parametrização.

Passo 4

Calcular

Como o problema não especifica a orientação da curva ou do vetor normal, vamos utilizar esse que encontramos mesmo.

Passo 5

Aplicar o Teorema

Onde é o círculo , como já vimos lá em cima.

Ok, como temos um círculo, a boa é usar coordenadas polares:

A região passa a ser então e . O que nos dá

Resposta

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k

Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d

Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi

Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .

Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê