Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 711234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697072737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 3, lista 3 - 2021.1, Questão 12c

( c ) Calcule ∫ γ v → ⋅ d r → onde v → ( x , y , z ) = ( x y + y ) i → + 2 y z j → + y 2 k → e γ é a intersecção do cilindro x 2 + y 2 = 4 com a superfície z = c o s ( y 2 ) + 5 orientada de modo que sua projeção no plano x y tenha sentido anti-horário.

Passo 1

Eaew, belezinha?

O enunciado nos pede para calcularmos a seguinte integração

∫ γ v → ⋅ d r →

em que temos o seguinte campo vetorial

v → ( x , y , z ) = ( x y + y ) i → + 2 y z j → + y 2 k →

e a curva pode ser obtida pela intersecção do cilindro

x 2 + y 2 = 4

com a superfície

z = c o s ( y 2 ) + 5

para isso, vamos utilizar o teorema de Stokes que faz a seguinte identificação

∫ γ v → ⋅ d r → = ∫ ∫ S r o t ( v → ) ⋅ n →   d S

Consegue ler a definição acima? Se não, vem comigo!

Passo 2

Para parametrizar a curva intersecção entre as duas superfícies, vamos usar coordenadas polares de forma que

x ( t ) = 2   c o s ( t ) e y ( t ) = 2   s e n ( t )

Desta forma, temos que

z ( t ) = c o s ( 4   s e n 2 ( t ) ) + 5

Ou seja, nossa curva é dada por

γ ( t ) = ( 2   c o s ( t ) ,   2   s e n ( t ) ,   c o s ( 4   s e n 2 ( t ) ) + 5 ) , 0 ≤ t ≤ 2 π

No entanto, com uma curva tão complicada, é mais conveniente analisarmos em termos do lado direito do teorema de Stokes, e calcularmos a integral de superfície! Vamos trabalhar com isso!

Passo 3

Vamos calcular as grandezas no lado direito do teorema de Stokes! Podemos começar com

r o t ( F → ) = ∇ → × F →

usando que ∇ → = ( ∂ ∂ x , ∂ ∂ y , ∂ ∂ x ) , e usando a fórmula para o produto vetorial, temos

r o t ( F → ) = ( ∂ F z ∂ y - ∂ F y ∂ z , ∂ F x ∂ z - ∂ F z ∂ x , ∂ F y ∂ x - ∂ F x ∂ y )

precisamos calcular todas as derivadas parciais! Vamos fazer uma de cada vez

∂ F z ∂ y = ∂ ∂ y [ y 2 ] = 2 y

Analogamente, vamos calcular as outras derivadas parciais

∂ F y ∂ z = ∂ ∂ z [ 2 y z ] = 2 y

∂ F x ∂ z = ∂ ∂ z [ x y + y ] = 0

∂ F z ∂ x = ∂ ∂ x [ y 2 ] = 0

∂ F y ∂ x = ∂ ∂ x [ 2 y z ] = 0

∂ F x ∂ y = ∂ ∂ y [ x y + y ] = x + 1

Portanto, nosso rotacional será

r o t ( F → ) = ( 2 y - 2 y , 0 - 0,0 - x - 1 ) = ( 0,0 , - x - 1 )

Ótimo! O rotacional ficou razoavelmente simples! Agora, precisamos do nosso vetor normal! Vamos lá!

Passo 4

A expressão do vetor normal pode ser obtida através do seguinte produto vetorial

n → = ∂ ϕ ( u , v ) ∂ u × ∂ ϕ ( u , v ) ∂ v

em que ϕ ( u , v ) é uma parametrização da superfície que tem como fronteira a curva que identificamos anteriormente, note que em nosso caso, é a própria superfície dada por

z = c o s ( y 2 ) + 5

se usarmos a parametrização

( x , y , z ) = ( r   c o s ( t ) , r   s e n ( t ) , c o s ( r 2 s e n 2 ( t ) ) + 5 )

temos que

∂ ϕ ( r , t ) ∂ r = [ c o s ( t ) , s e n ( t ) , - 2   r   s e n 2 ( t )   s e n ( r 2 s e n 2 ( t ) ]

agora para a derivada em relação a t temos que

∂ ϕ ( r , t ) ∂ t = [ - r   s e n ( t ) , r   c o s ( t ) ,   - 2 r 2 s e n ( t ) c o s ( t ) s e n ( r 2 s e n 2 ( t ) ) ]

Aplicando a definição de produto vetorial temos que

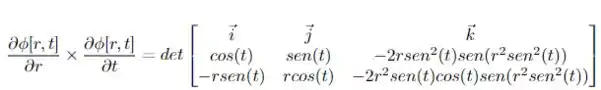
aplicando o determinante, temos então que

n → = ( 0 ,   2 r 2 s e n ( t ) s e n ( r 2 s e n 2 ( t ) ) [ c o s 2 ( t ) - s e n 2 ( t ) ] ,   r   )

Agora, vamos voltar para a nossa integral!

Passo 5

A integral é tal que

∫ γ F → ⋅ d r → = ∫ ∫ S r o t ( F → ) ⋅ n →   d S

temos que a parametrização foi feita em ( r , t ) , portanto d S = d r d t , ou seja

∫ γ F → ⋅ d r → = ∫ ∫ S ( 0,0 , - r   c o s ( t ) - 1 ) ⋅ ( 0 ,   2 r 2 s e n ( t ) s e n ( r 2 s e n 2 ( t ) ) [ c o s 2 ( t ) - s e n 2 ( t ) ] ,   r   ) d S

em que usei x = r   c o s ( t ) . Sendo assim, a nossa integral se torna

∫ γ F → ⋅ d r → = ∫ 0 2 π ∫ 0 2 ( - r 2 c o s ( t ) - r ) d r d t

Vamos tentar resolver ela agora!

Passo 6

Integrando individualmente em t , temos que

∫ 0 2 π ∫ 0 2 ( - r 2 c o s ( t ) - r ) d r d t = - ∫ 0 2 r 2 [ ∫ 0 2 π c o s ( t ) d t ] d r - ∫ 0 2 [ ∫ 0 2 π d t ] d r

usando a integral conhecida para o cosseno, temos que

∫ 0 2 π c o s ( t ) d t = s e n ( t ) | 0 2 π = 0

e, temos que

∫ 0 2 π d t = t | 0 2 π = 2 π

Nos deixando apenas com

∫ 0 2 π ∫ 0 2 ( - r 2 c o s ( t ) - r ) d r   d t = - 2 π ∫ 0 2 d r

resolvendo a integral que falta

∫ 0 2 d r = r | 0 2 = 2

temos finalmente que

∫ γ F → ⋅ d r → = - 4 π

Que é o resultado que queríamos obter! A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

∫ γ F → ⋅ d r → = - 4 π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê