Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 391234567891011121314151617181920212223242526272829303132333435363738404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Seja C a curva intersecção do cilindro de equação x 2 + y 2 = 1 com o paraboloide hiperbólico z = 2 x y

(a) Parametrize C positivamente

(b) Calcule o rotacional do campo F → x , y , z = y + sen ⁡ x i → + z 2 + cos ⁡ y j → + x 3 k → .

(c) Calcule

∫ C y + sen ⁡ x d x + z 2 + cos ⁡ y d y + x 3 d z

Passo 1

Letra (a)

Pra parametrizar essa curva aqui, nem precisamos do esboço, olha só como podemos fazer:

Sabemos que a curva está no cilindro x 2 + y 2 = 1 , com isso

x = cos ⁡ t

y = sen ⁡ t

0 ≤ t ≤ 2 π

Perceba que é só um parâmetro mesmo, estamos querendo uma curva!

A segunda equação nos diz como z está presente nesse cilindro

z = 2 x y

z = 2 cos ⁡ t sen ⁡ t

Pronto, é isso

C : σ t = cos ⁡ t , sen ⁡ t , 2 cos ⁡ t sen ⁡ t

0 ≤ t ≤ 2 π

Se você estava muito curioso de como é essa curva, o esboço é esse aqui:

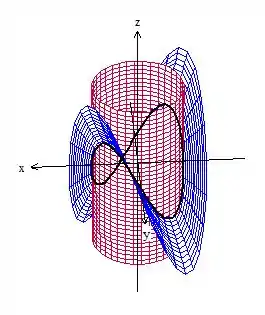
A ideia foi mostrar que nem sempre a gente precisa conseguir desenhar a figura, então na prova se estiver muito difícil conseguir um esboço, não se desespere! =D

Passo 2

Letra (b)

Rotacional de um campo, lembra como calcula isso?

r o t F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z , ∂ F 1 ∂ z - ∂ F 3 ∂ x , ∂ F 2 ∂ x - ∂ F 1 ∂ y

O campo que o enunciado pede o rotacional é esse aqui

F → x , y , z = y + sen ⁡ x i → + z 2 + cos ⁡ y j → + x 3 k →

Logo

F 1 = y + sen ⁡ x

F 2 = z 2 + cos ⁡ y

F 3 = x 3

O rotacional vai ser

r o t F → = 0 - 2 z , 0 - 3 x 2 , 0 - 1

r o t F → = - 2 z , - 3 x 2 , - 1

É só isso que a letra (b) pede pra gente mesmo.

Passo 3

Letra (c)

Agora começa a ficar complicada a parada, como vamos calcular a integral de linha desse campo bizarro nessa curva bizarra?

Pelo método direto vai ser impossível né?

Como o enunciado já fez a gente calcular o rotacional e ele não é tão complexo, vamos tentar usar o teorema de Stokes aqui, ele diz

∬ S r o t F → . n → d S = ∮ C F → d r →

Onde C = ∂ S , ou seja, C é a fronteira de uma superfície S . Só precisamos escolher essa superfície.

Bom, podemos escolher o próprio pedaço do hiperboloide que está dentro do cilindro, ele com certeza tem essa curva C como fronteira, olha o esboço

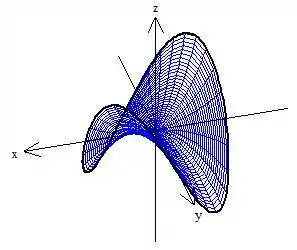
O hiperboloide é definido por z = 2 x y e queremos a região dentro do cilindro x 2 + y 2 = 1 , portanto

S : φ x , y = x , y , 2 x y

x 2 + y 2 ≤ 1

Passo 4

Precisamos da normal à essa superfície ainda

N → = ∂ φ ∂ x × ∂ φ ∂ y

∂ φ ∂ x = 1,0 , 2 y

∂ φ ∂ y = 0,1 , 2 x

N → = i j k 1 0 2 y 0 1 2 x

N → = - 2 y , - 2 x , 1

Pela regra da mão direita, como nossa curva está orientada no sentido anti-horário, precisamos da normal apontada pra cima mesmo, portanto esse vetor normal é o que queremos.

Precisamos escrever o rotacional de F → com os novos parâmetros também, isto é

x = x

y = y

z = 2 x y

O rotacional fica

r o t F → = - 2 z , - 3 x 2 , - 1

r o t F → = - 4 x y , - 3 x 2 , - 1

O teorema de Stokes fica assim

∮ C F → d r → = ∬ x 2 + y 2 ≤ 1 - 4 x y , - 3 x 2 , - 1 . - 2 y , - 2 x , 1 d x d y

= ∬ x 2 + y 2 ≤ 1 8 x y 2 + 6 x 3 - 1 d x d y

Passo 5

Pra resolver essa integral com esse limite, precisamos fazer uma mudança para coordenadas polares

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

Substituindo na integral

∫ 0 2 π ∫ 0 1 ( 8 r cos ⁡ θ r sen ⁡ θ 2 + 6 r cos ⁡ θ 3 - 1 ) r d r d θ

= ∫ 0 2 π ∫ 0 1 8 r 4 cos ⁡ θ sen 2 ⁡ θ + 6 r 4 cos 3 ⁡ θ - r d r d θ

Integrando em r

∫ 0 2 π 8 r 5 5 cos ⁡ θ sen 2 ⁡ θ + 6 r 5 5 cos 3 ⁡ θ - r 2 2 d θ

= ∫ 0 2 π 8 5 cos ⁡ θ sen 2 ⁡ θ + 6 5 cos 3 ⁡ θ - 1 2 d θ

Vamos fazer cada uma dessas três integrais separadamente, olha só

∫ cos ⁡ θ sen 2 ⁡ θ d θ

u = sen ⁡ θ

d u = cos ⁡ θ

∫ u 2 d u = u 3 3

∫ cos ⁡ θ sen 2 ⁡ θ d θ = sen 3 ⁡ θ 3

A segunda é um pouco mais trabalhosa

∫ cos 3 ⁡ θ d θ = ∫ cos ⁡ θ cos 2 ⁡ θ d θ

= ∫ cos ⁡ θ 1 - sen 2 ⁡ θ d θ

= ∫ cos ⁡ θ - sen 2 ⁡ θ cos ⁡ θ d θ

∫ cos 3 ⁡ θ d θ = sen ⁡ θ - sen 3 ⁡ θ 3

A terceira vou botar aqui só pra gente não esquecer mesmo

∫ 1 2 d θ = θ 2

Juntando tudo isso

∫ 0 2 π 8 5 cos ⁡ θ sen 2 ⁡ θ + 6 5 cos 3 ⁡ θ - 1 2 d θ =

= 8 5 . sen 3 ⁡ θ 3 + 6 5 sen ⁡ θ - sen 3 ⁡ θ 3 - θ 2 0 2 π

Só que sen ⁡ 2 π = sen ⁡ 0 = 0 , então some quase tudo!

= 0 + 0 - 2 π 2 = - π

∮ C F → d r → = - π

Resposta

(a)

C : σ t = cos ⁡ t , sen ⁡ t , 2 cos ⁡ t sen ⁡ t

0 ≤ t ≤ 2 π

(b)

r o t F → = - 2 z , - 3 x 2 , - 1

(c)

∮ C F → d r → = - π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê