Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 431234567891011121314151617181920212223242526272829303132333435363738394041424445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere o campo vetorial F → x ,   y ,   z = x j → + x y k →   e S a superfície descrita pelas relações x 2 + y 2 + z 2 4 = 1 e z ≤ 1 , orientada de modo que o vetor normal no ponto 0 ,   0 ,   - 2 esteja apontando para baixo.

  1. Esboce a superfície S .
  2. Determine a curva que forma a fronteira de S e oriente-a positivamente.
  3. Calcule o fluxo do rotacional de F → através de S .

Passo 1

Letra a) Antes de desenharmos a superfície S em si, vamos entender melhor as componentes dela, ou seja, o que representa essas duas relações?

A primeira delas, x 2 + y 2 + z 2 4 = 1 , nos representa um elipsoide, se lembra?

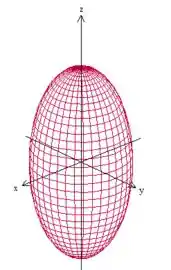
Esse elipsoide alongado em z corta o eixo z (fazendo x = 0 e y = 0 ) em

x 2 + y 2 + z 2 4 = 1   →

z 2 = 4

z = ± 2

z = 2 é o ponto em cima e z = - 2 em baixo.

Bem, mas essa ainda não é a superfície S , pois a S tem uma restrição: z ≤ 1 , ou seja, vamos cortar esse paraboloide por um plano que passa por z = 1

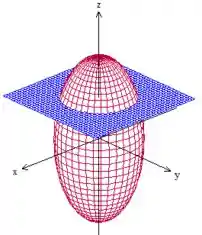
E pegaremos somente a parte de baixo

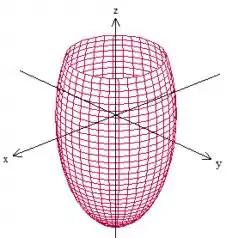
E eis aí a superfície S ! ;)

Passo 2

Letra b) Para determinar aquela curva que delimita S ali em cima, vamos fazer o mesmo que fizemos graficamente: vamos cortar o elipsoide com o plano z = 1 , mas agora nas fórmulas. Bora?

x 2 + y 2 + z 2 4 = 1           ⇒ s b s b s t i t u i n d o   o   z   d o   p l a n o           x 2 + y 2 + 1 2 4 = 1

Simplificando

x 2 + y 2 = 1 - 1 4       →

x 2 + y 2 = 3 4

Como podemos desconfiar graficamente, a intersecção é uma esfera de raio 3 / 2 .

Passo 3

Pois bem, entes de parametrizar, vamos orienta-la do jeito pedido, pois aí a gente procura uma parametrização com essa orientação.

De acordo com o enunciado, devemos ter que o vetor normal a superfície no ponto ( 0 ,   0 ,   - 2 ) tem que estar para baixo

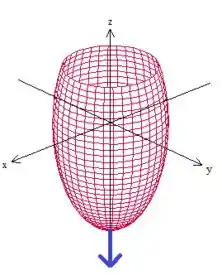
Bem, se levarmos esse vetor lá pra cima sem inverter a orientação

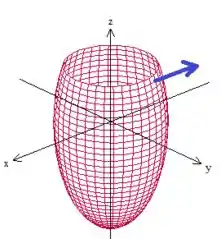
e utilizarmos a regra da mão direita para orientar a curva

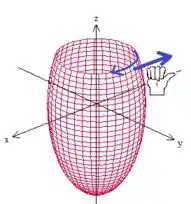
Percebemos então que ela gira no sentido horário vista de cima pra baixo

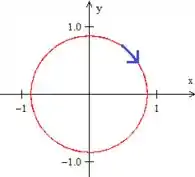
Passo 4

Bem, uma parametrização legal para essa curva que segue essa orientação seria comparando com a parametrização polar:

x = r sin ⁡ θ           ⇒ s u b s t i t u i n d o   o   r a i o   d a   c u r v a           x = 3 2 sin ⁡ θ

y = r cos ⁡ θ         ⇒ s u b s t i t u i n d o   o   r a i o   d a   c u r v a           y = 3 2 cos ⁡ θ

Mas note que invertemos o x e o y apenas para a curva seguir essa orientação.

Como essa curva está no plano z = 1

Ficamos com a parametrização

σ θ = 3 2 sin ⁡ θ ,   3 2 cos ⁡ θ ,   1

Onde o parâmetro θ

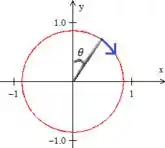
Varia de 0 ≤ θ ≤ 2 π

E repare mais uma vez que essa parametrização atende a orientação !

Passo 5

Letra c) Primeiro, vamos ver o que de fato queremos, ou seja

∬ S   r o t   F → ∙ n →   d S

Bem, calcular essa integral de superfície, não rola, pois essa superfície é muito chata de parametrizar, certo?

Então vamos contornar o problema utilizando o teorema de Stokes:

∬ S   r o t   F → ∙ n →   d S = ∫ C   F → d r →

Onde C é a curva fechada bordo de S , ou seja... é a curva que acabamos de encontrar que já está até parametrizada, percebeu? Então bora calcular essa integral de linha e matar a questão por Stokes!:)

Passo 6

Encontrando primeiro d r → pela relação

d r → = σ ' d θ

Bastando então derivar termo a termo da parametrização σ θ = 3 2 sin ⁡ θ ,   3 2 cos ⁡ θ ,   1 :

d r → = 3 2 cos ⁡ θ ,   - 3 2 sin ⁡ �� ,   0 d θ

Passo 7

Jogando tudo isso na integral de linha, lembrando que F → x ,   y ,   z = x j → + x y k → , ou melhor F → = 0 ,   x ,   x y ...

∫ C   F → d r → = ∫ 0 2 π   0 ,   x ,   x y ∙ 3 2 cos ⁡ θ ,   - 3 2 sin ⁡ θ ,   0 d θ

Efetuando esse produto interno

∫ C   F → d r → = ∫ 0 2 π - x 3 2 sin ⁡ θ   d θ

Como estamos integrando em θ não podemos ter x , logo o substituiremos pela parametrização   x = 3 2 sin ⁡ θ :

∫ C   F → d r → = ∫ 0 2 π - 3 2 sin ⁡ θ 3 2 sin ⁡ θ   d θ →

∫ 0 2 π - 3 4 sin 2 ⁡ θ   d θ

Lembrando que sin 2 ⁡ θ = 1 - cos ⁡ 2 θ 2 ,

- 3 4 ∫ 0 2 π 1 - cos ⁡ 2 θ 2   d θ =

- 3 8 ∫ 0 2 π 1 - cos ⁡ 2 θ   d θ

Integrando em θ da constante

- 3 8 2 π - ∫ 0 2 π cos ⁡ 2 θ d θ

fazendo uma substituição simples de 2 θ = a

d a = 2   d θ →

d θ = d a 2

Não se esquecendo de mudar também os limites

θ = 0           →             a = 2 ∙ 0 = 0

θ = 2 π           →             a = 2 ∙ 2 π = 4 π

Logo

- 3 8 2 π - ∫ 0 2 π cos ⁡ 2 θ d θ =

- 3 8 2 π - ∫ 0 4 π cos ⁡ a d a =

- 3 8 2 π - sin ⁡ a 0 4 π =

Substituindo os limites esse seno zera, portanto

- 3 4 π

Resposta

Letra a)

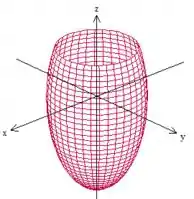
Letra b)

x 2 + y 2 = 3 4

G i r a   n o   s e n t i d o   h o r á r i o   v i s t a   d e   c i m a

Letra c)

∬ S   r o t   F → ∙ n →   d S = - 3 4 π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê