Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 351234567891011121314151617181920212223242526272829303132333436373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Use o teorema de Stokes para calcular o trabalho W = ∫ δ S F ⋅ d r → realizado pelo campo de força

F x , y , z = - 3 y 2   i → + 4 z   j → + 6 x   k →

Onde S é a superfície orientável, com fronteira δ S orientada positivamente, definida pela parametrização

r u , v = u , v , v 2 ,   u , v ∈ D

Com D o triângulo de vértices 2,0 ,   0,2 e 0,0 .

Passo 1

Esse trabalho é uma integral de linha vetorial. O Teorema de Stokes diz que:

W = ∮ δ S F ⋅ d r → = ∫ ∫ S r o t   F ⋅ n → d s

S é a nossa superfície e δ S é a fronteira da nossa superfície, assim como o enunciado fala. Então a ideia é que a gente só precisa montar e calcular a integral da direita, para então achar o valor da esquerda. Maneiro, né?

Maaas a gente precisa atender a alguns critérios para podermos aplicar esse teorema antes de começar:

1. Nossa fronteira precisa estar orientada positivamente em relação a superfície. E isso já está acontecendo, o enunciado disse para a gente!

2. O campo precisa estar bem definido para o domínio de integração. Olha ele:

F x , y , z = - 3 y 2   i → + 4 z   j → + 6 x   k →

Não tem nenhum ponto de descontinuidade aí né (nenhum denominador que possa zerar ou algo assim). Então a gente pode confiar que ele está bem definido para o nosso domínio de integração, já que ele está bem definido para todos os valores de x , y , z .

Então, tá belezinha, a gente pode usar o teorema sem preocupações. Bora lá!

Passo 2

Vamos montar nossa integral de superfície lindona:

∫ ∫ S r o t   F ⋅ n → d s

Começando por r o t   F . Esse cara é o rotacional do nosso campo. Ele tem essa fórmulinha:

r o t   F → = i ^ j ^ k ^ ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3

Nosso campo é:

F = F 1 , F 2 , F 3 = ( - 3 y 2 , 4 z , 6 x )

Então precisamos calcular:

r o t   F → = i ^ j ^ k ^ ∂ ∂ x ∂ ∂ y ∂ ∂ z - 3 y 2 4 z 6 x

r o t   F → = ∂ 6 x ∂ y - ∂ 4 z ∂ z i ^ - ∂ 6 x ∂ x - ∂ - 3 y 2 ∂ z j ^ + ∂ 4 z ∂ x - ∂ - 3 y 2 ∂ y k ^

r o t   F → = 0 - 4 i ^ - 6 - 0 j ^ + 0 - ( - 6 y ) k ^

r o t   F → = - 4 , - 6 ,   6 y

Nossa integral fica:

∫ ∫ S - 4 , - 6,6 y ⋅ n → d s

Passo 3

Agora a gente precisa calcular n → que são os vetores normais a superfície que a orientam positivamente. A gente o acha pela parametrização da superfície que ele deu:

r u , v = u , v , v 2

∂ r ∂ u = 1,0 , 0

∂ r ∂ v = 0,1 , 1 2

n → = ∂ r ∂ u × ∂ r ∂ v = i ^ j ^ k ^ 1 0 0 0 1 1 / 2

N → = 0 , - 1 2 ,   1

Mas a gente precisa verificar se ele tá na orientação certa. Como assim? Para usar esse teorema, nossa superfície precisa estar orientada positivamente em relação a fronteira

A gente tem o nosso vetor com a coordenada z positiva. Então ele está sempre virado para cima. Aí pensa comigo, se o vetor está para cima, pela regra da mão direita, nossa curva precisa estar sendo percorrida no sentido anti-horário. Olha só:

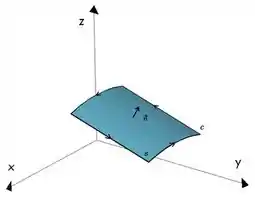
Nessa imagem a gente tem uma superfície genérica orientada positivamente. Aí repara: vetor para cima e sentido anti-horário.

Então nosso vetor tá certinho, considerando que nossa curva está no sentido anti-horário. Vamos colocar ele na integral

∫ ∫ S - 4 , - 6,6 y ⋅ 0 , - 1 2 ,   1 d s = ∫ ∫ S 3 + 6 y d s

Passo 4

Vamos definir nossos extremos de integração. Eles vão descrever o domínio em que nossa superfície está parametrizada, ou seja o triângulo de vértices 2,0 ,   0,2 e 0,0 em u , v . Vamos desenhar esse bonito:

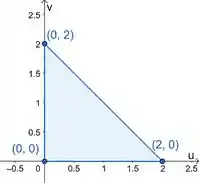
Agora vamos limitar as variáveis u e v , para achar nossos extremos de integração. No eixo u , vemos que ele está entre:

0 ≤ u ≤ 2

Já no eixo v , ele é limitado por baixo por v = 0 e por cima pela reta que passa por ( 2 , 0 ) e ( 0 , 2 ) . Achando a equação dessa reta pela fórmulinha (cê pode fazer do jeito que achar melhor, tá?)

v - v 0 = m u - u 0

Sendo

m = Δ v Δ u = 2 - 0 0 - 2 = - 1

E escolhendo

u 0 , v 0 = 2 , 0

∴

v - 0 = - 1 u - 2 ∴ v = - u + 2

Aí dizemos que:

0 ≤ v ≤ - u + 2

Passo 5

Agora é montar a integral.

W = ∮ δ S F ⋅ d r → = ∫ ∫ S r o t   F ⋅ n → d s

∴

W = ∮ δ S F ⋅ d r → = ∫ ∫ S 3 + 6 y d s

W = ∮ δ S F ⋅ d r → = ∫ 0 2 ∫ 0 - u + 2 3 + 6 y d v d u

Mas repara que nosso domínio de integração está em u v , então a gente não pode integrar com aquele y ali. O que a gente faz então? Bora lembrar da nossa parametrização:

r u , v = u , v , v 2

Repara na componente y dela:

y = v

Bora substituir isso na integral:

W = ∮ δ S F ⋅ d r → = ∫ 0 2 ∫ 0 - u + 2 3 + 6 v d v d u

Passo 6

Bora calcular essa belezura:

W = ∮ δ S F ⋅ d r → = ∫ 0 2 ∫ 0 - u + 2 3 + 6 v d v d u

= ∫ 0 2 3 v + 6 2 v 2 0 - u + 2 d u = ∫ 0 2 - 3 u + 6 + 3 - u + 2 2 d u

∫ 0 2 - 3 u + 6 + 3 u 2 - 12 u + 12 d u = ∫ 0 2 3 u 2 - 15 u + 18 d u

= 3 3 u 3 - 15 2 u 2 + 18 u 0 2 = 8 - 30 + 36 = 14

E finalmente a gente pode dizer que:

W = ∮ δ S F ⋅ d r → = 14

Resposta

W = ∮ δ S F ⋅ d r → = 14

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê