Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 512346789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Use o teorema de Stokes para mostrar que a integral de linha é igual ao valor dado, indicando a orientação da curva C .

∮ C   8 x - 2 y d x + y d y + 3 z d z = 4 3

onde C é a fronteirado triângulo equilátero situado no plano - 3 x + 3 z + 6 = 0 de vértices P = 2,2 , 0 ,   Q = ( 2,6 , 0 ) e R = ( 2 + 3 , 4,3 )

Passo 1

Primeiro devemos encontrar a função vetorial em questão e o seu rotacional. Temos que F → = ( 8 x - 2 y ,   y ,   3 z ) e o rotacional pode ser calculado por:

∇ ×   F → = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3

∇ ×   F → = ( 0 ,   0 ,   2 )

Passo 2

Agora vamos encontrar a normal a superfície, esta superfície pode ser parametrizada de forma explícita como:

z = f x , y = 3 x - 6 3

Assim,

N → x , y = - ∂ f ∂ x x , y ,   - ∂ f ∂ y x , y ,   1

N → x , y = - 3 3 ,   0 ,   1

Passo 3

Vamos aplicar o teorema de Stokes ∮ ∂ S   F → . d r = ∬ S   ∇ ×   F → . n → d S = ∬ S   ∇ ×   F → . N → d x d y

Substituindo pelo rotacional e pela normal que calculamos, temos:

∬ S   ∇ ×   F → . N → d x d y =   ∬ S   0,0 , 2 . - 3 3 ,   0 ,   1 d x d y = ∬ S   2 d x d y

Mas, ∬ S   2 d x d y , representa o dobro da área da superfície projetada no plano x y . Não confunda isso! Quando temos “ d x d y ” ali do lado, estamos falando de tudo no plano x y já, beleza?

Passo 4

O último passo é calcular a área da superfície! Sorte nossa que é um triângulo! Esse aqui é o triângulo original da questão, ele está em 3 D :

R = 2 + 3 , 4,0

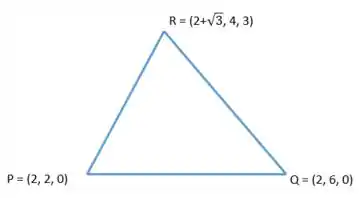
Precisamos projetar ele no plano x y pra calcular a área, mas isso é simples: só zerar os termos em z . No caso fica assim

R ' = 2 + 3 , 4

P = 2,2

Q = 2,6

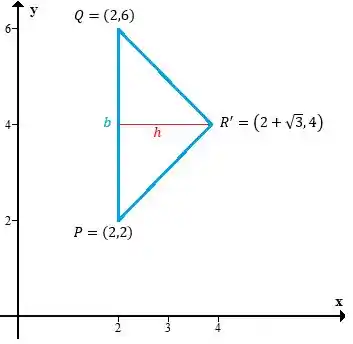
O lado P Q tem medida igual a 4 pois os dois pontos estão no plano x y e sobre a reta x = 2 , então a distância entre eles é a diferença entre a coordenada y .

A altura aqui também está sobre a reta y = 4 , portanto o seu tamanho vai ser dado pela diferença nas coordenadas de x , logo h = 2 + 3 - 2

h = 3

Logo, a área do triângulo é:

A = b h 2

A = 4 . 3 2 = 2 3

Então,

2 A = 4 3

E aproveitando a imagem aí em cima e sabendo que a normal que escolhemos aponta para o x negativo, nós temos a orientação da curva C ! Que no caso é Q → P → R → Q .

Resposta

Assim, a integral de linha do camp F → definido no enunciado é dada por:

∮ C   F → . d r = 2 A = 4 3

E a orientação usada foi Q → P → R → Q

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê