Considere a superfície que é a parte do elipsoide que está acima do plano e com os vetores normais apontando para fora. Seja e
- Use o teorema de Stokes para calcular , calculando uma integral de superfície.
- Use o teorema de Stokes para calcular , calculando uma integral de linha.
Passo 1
Antes de tudo, vamos desenhar essa superfíce, para entender um pouco melhor o que está acontecendo. Temos um elipsoide cortado pelo plano :
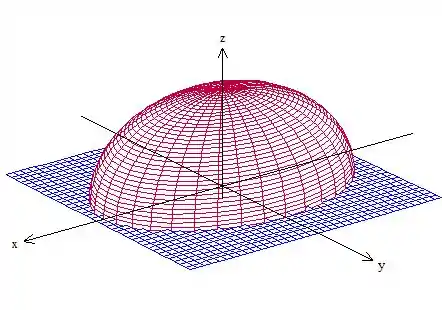 .
.
Passo 2
Letra a)
Agora, o enunciado pede para a gente calcular
Usando o Teorema de Stokes, calculando uma integral de superfície. O que ele quer dizer com isso?
É só calcular a integral de superfície que ele pediu mesmo, no elipsoide? Vamos pensar um pouco.
O Teorema de Stokes nos diz que a integral de superfície do rotacional de em uma superfície (isso é o do problema) é igual à uma integral de linha de na fronteira de , que, no caso, já deu para ver que é uma elipse.
Ou seja, qualquer superfície que tenha essa elipse como fronteira nos dá a mesma integral de superfície.
Isso quer dizer que podemos trocar a superfície do problema (o elipsoide cortado) por uma outra mais simples que tenha a mesma elipse como fronteira, inclusive, a própria elipse plana, contida no plano .
Foi? Resumindo: aplicando o Teorema de Stokes, concluímos que qualquer superfície que tenha a mesma borda de nos dá a mesma integral de superfície, então, escolhemos essa seção do plano que preenche essa elipse.
Podemos escrever, então
Onde é essa elipse plana contida no plano .
Passo 3
Beleza, agora vamos calcular isso aí.
Primeiro, vamos parametrizar nossa nova superfície e calcular seu vetor normal. Como a elipse está contida no plano , podemos parametrizá-la como:
Onde os parâmetros e devem estar “dentro” da projeção da superfície no plano , ou seja, dentro da elipse.
Fazendo a interseção do elipsoide com o plano , temos:
Como queremos os pontos que estão dentro da elipse, temos:
Passo 4
Esse é o domínio da superfície . Agora vamos calcular a normal dessa superfície.
Como o problema diz que os vetores normais apontam para fora no elipsoide (ou seja, para cima), para manter o sentido vetorial correto, eles devem apontar para cima no plano. Como o vetor que encontramos possui a coordenada positiva, quer dizer que ele está no sentido correto!
Passo 5
Agora, vamos calcular o rotacional de . Temos:
Escrevendo o rotacional em termos das variáveis da parametrização, temos:
Legal, deu no mesmo -.-
Ok, vamos continuar.
Passo 6
Agora, vamos montar a integral de superfície
Onde é dado por
O domínio da parametrização. Vamos calcular isso aí então:
Olha que maravilha, nem precisamos fazer mais conta : )
Passo 7
Letra b)
Agora, temos que calcular usando uma integral de linha. Pelo Teorema de Stokes, a integral de superfície que o problema pede é igual à integral de linha de na elipse que forma a fronteira de , ou seja:
Onde , como nós já vimos, é dada pela elipse de equação
Cuidado para não se confundir. Na letra ), nós estávamos falando da superfície em forma de elipse (portanto, de uma integral de superfície), agora, estamos falando da curva em forma de elipse (portanto, uma integral de linha).
Para calcular essa integral de linha, vamos usar a fórmula
Passo 8
Precisamos, então, parametrizar essa curva. Já que temos uma elipse, vamos usar coordenadas elípticas, né
Temos uma elipse em .
Esse coeficiente está ali para cortar o do denominador de na equação da elipse , para podermos encontrar a indentidade trigonométrica .
Bom, como temos uma volta completa, vai de a . Tá certo isso?
Temos que tomar extremo cuidado com a orientação vetorial aqui. Se o problema fala que a normal aponta para fora, pela regra da mão direita, vemos que a curva deve ser percorrida no sentido anti-horário. Então, vai de fato de a .
Agora, vamos derivar a parametrização que encontramos:
Passo 9
Vamos montar a integral de linha. Escrevendo o campo em termos das variáveis da parametrização ,temos:
Susbstituindo na integral,
O intervalo de veio da parametrização, ok?
Bom, graças a Deus que deu zero de novo, né?! Show, é isso aí, gente.