Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 921234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909193949596979899100

Enunciado

UNICAMP. Calculo 2. 2021.2 - 5ª Tarde. Prova: P3. Questão 3.

Use o Teorema de Stokes para calcular a integral de linha ∫ C F · d r , onde

F x , y , z = x 2 y i + 1 3 x 3 j + x y k

e C é a interseção do paraboloide hiperbólico z = y 2 - x 2 com o cilindro x 2 + y 2 = 1 , com orientação no sentido anti-horário quando vista de cima.

Passo 1

Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Para essa questão, foi dada uma função vetorial F e foi pedido para que usemos o Teorema de Stokes para calcular a integral ∫ C F · d r onde C é a interseção do paraboloide z = y 2 - x 2 com o cilindro x 2 + y 2 = 1 , cuja orientação é no sentido anti-horário visto de cima.

Parece muita informação, não é?

Mas como podemos aplicar este teorema aqui? 🤔🤔

O Teorema de Stokes diz que

∫ C F · d r = ∬ C R o t F · N d A

No caso, R o t F é dado pela matriz

R o t F = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3

Dado que F = F 1 i + F 2 j + F 3 k e N é um vetor normal a C .

Entendeu? Bora começar! 😁😁

Passo 2

Primeiro de tudo, temos que parametrizar a superfície passando de três variáveis para duas.

Podemos fazer isso assumindo x como x , y como y e como z = y 2 - x 2 , não precisamos fazer nada, ou seja

ϕ x , y = x , y , y 2 - x 2

Mas talvez você esteja se perguntando, “e o cilindro x 2 + y 2 = 1 ?”

Calma, vamos usar ele mais tarde para definir os limites de integração.

Já que encontramos ϕ x , y , vamos pular uma parte e calcular N logo

Um vetor normal a uma parametrização como essa é dado como o produto vetorial das derivadas parciais de ϕ x , y , ou seja

N = ∂ ϕ x , y ∂ x X ∂ ϕ x , y ∂ y

Calculando a derivada parcial de ϕ com relação a x , temos

∂ ϕ x , y ∂ x = ∂ x , y , y 2 - x 2 ∂ x

Pelo método de derivação polinomial

∂ ϕ x , y ∂ x = 1,0 , - 2 x

Agora a derivada parcial de ϕ com relação a y

∂ ϕ x , y ∂ y = ∂ x , y , y 2 - x 2 ∂ y

Pelo mesmo método de derivação

∂ ϕ x , y ∂ y = 0,1 , 2 y

Com isso, N é dado por

N = i j k 1 0 - 2 x 0 1 2 y = 2 x , - 2 y , 1

Tranquilo até aqui? 😉

Passo 3

Agora vamos calcular o rotacional de F . Como vimos no passo 1, R o t F é dado por

R o t F = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3

Sendo que F = F 1 i + F 2 j + F 3 k , ou seja F 1 = x 2 y , F 2 = 1 3 x 3 e F 3 = x y

R o t F = ∂ F 3 ∂ y - ∂ F 2 ∂ z i + ∂ F 1 ∂ z - ∂ F 3 ∂ x j + ∂ F 2 ∂ x - ∂ F 1 ∂ y k

Substituindo F 1 , F 2 e F 3

R o t F = ∂ x y ∂ y - ∂ 1 3 x 3 ∂ z i + ∂ x 2 y ∂ z - ∂ x y ∂ x j + ∂ 1 3 x 3 ∂ x - ∂ x 2 y ∂ y k

Vamos calcular as derivadas.

Podemos ver que as derivadas ∂ 1 3 x 3 ∂ z e ∂ x 2 y ∂ z são iguais a 0 já que não temos z para derivar em suas funções.

Já as outras derivadas são obtidas pelo método de derivação polinomial.

∂ x y ∂ y = x y 1 - 1 = x

∂ x y ∂ x = x 1 - 1 y = y

∂ 1 3 x 3 ∂ x = 3 1 3 x 3 - 1 = x 2

∂ x 2 y ∂ y = x 2 y 1 - 1 = x 2

Substituindo os resultados em R o t F

R o t F = x - 0 i + 0 - y j + x 2 - x 2 k

Simplificando, temos

R o t F = x i - y j + 0 k

Ou podemos escrever como

R o t F = x , - y , 0

Interessante, não é? 😁

Passo 4

Agora substituímos R o t F e N na integral

∬ C R o t F · N d A

∬ C x , - y , 0 · 2 x , - 2 y , 1 d A

Calculando esse produto interno, temos

∬ C 2 x 2 + 2 y 2 d A

∬ C 2 x 2 + y 2 d A

Agora vamos olhar para C , no caso, C é a interseção da superfície com o cilindro. Por esse teorema, vamos olhar para a projeção da interseção no plano x y .

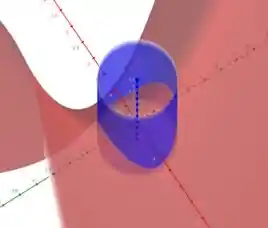
A projeção de C no plano x y é uma circunferência de raio 1 .

Logo vemos que C pode ser calculado como coordenadas polares.

Lembra como fazemos essa transformação?

x = r c o s θ y = r s e n θ x 2 + y 2 = r 2 J a c o b i a n o = r

Convertendo nossa integral para esse modelo

∬ C 2 r 2 r d A

Ok, mas e os limites de integração?

No caso, r é fixo em 1 já que x 2 + y 2 = 1 , e θ varia entre 0 a 2 π já que estamos dando a volta completa em torno da origem do sistema.

∬ C 2 1 2 1 d A = ∬ C 2 d A = 2 ∬ C d A

Logo, a integral de linha que procuramos é 2 · Á r e a   d a   C i r c u n f e r ê n c i a

Sabemos que a área da circunferência é dada por A = π r 2 , como r = 1

A = π

Por tanto

∬ C R o t F · N d A = 2 π

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

∬ C R o t F · N d A = 2 π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê