Seja
1. Calcule o campo gradiente
2. Seja a parte da esfera que satisfaz , orientada de forma que seja seu vetor normal no ponto . Denote o bordo de orientado positivamente. Esboce a superfície e a curva com as orientações indicadas.
3. Defina o campo vetorial
Onde foi calculado no item . Dada a supefície do item , calcule o fluxo do campo através de .
Passo 1
1.
Bem aqui vamos só usar um conceito que aprendemos lá em Cálculo e lembrar que o gradiente é, simplesmente:
E calculando um por um, temos:
Então, fica meio feio mas foi o que a questão pediu:
Passo 2
2.
Aqui é só pra desenhar, então vamos começar com a esfera toda:
Mas ele diz que só o pedaço , então só pegamos mesmo essa parte em vermelho aqui:
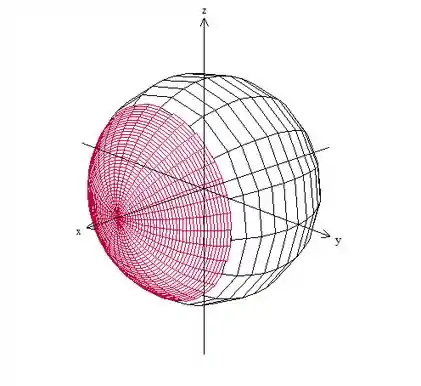
Agora só temos que fazer a curva da fronteira com orientação certa, seguindo aregra da mão direita. No final, vamos ter algo assim:
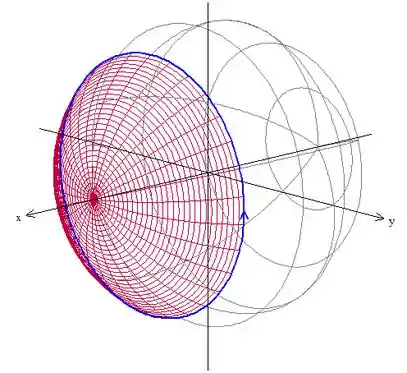
Onde, só pra deixar bem claro, é a parte em vermelho da superfície e a curva em azul.
Passo 3
3.
Agora as coisas complicam um pouco mais e ele ainda pede a integral... Mas calma que fazendo tudo no passo-a-passo nao vai ter erro!
Temos o campo:
Onde é aquele campo bizarrinho que encontramos lá em cima. Esse outro pedaço eu vou chamar de só pra facilitar e não nos confundirmos no caminho.
Agora temos que calcular o rotacional de , mas essa conta parece muito chata, né?
Calma que agora vamos lembrar de algo que vai facilitar tudo! Não foi o exercício mesmo que disse que o campo é o gradiente de uma função escalar? Então, isso é dizer que o campo é conservativo! E campos conservativos tem rotacional nulo.
Na hora da conta, o que vamos ter vai ser simplesmente:
Que é consideravelmente tranquilo de calcular. Vamos ver!
Passo 4
O rotacional é o produto vetorial do operador com o campo, então:
É ou não é um valor muito simpático, hein? Haha
Agora é só calcularmos a integral!
Passo 5
Vamos logo ao que ele pede mesmo, que é a integral do fluxo do rotacional de sobre :
Poderíamos já tentar calcular essa integral diretamente aí, já que nem a superfície nem o campo são muito complicados, mas aqui vamos usar um macetezinho do teorema de Stokes, já que essa integral do fluxo do rotacional é exatamente a integral que aparece lá no teorema:
E a fronteira , no caso, é a circunferência, que desenhamos lá no item :
O legal é que a nossa superfície com certeza não é a única que tem essa fronteira, então podemos fazer:
E escolhermos uma outra superfície de mesma fronteira qualquer que seja mais simples ainda de se calcular. No caso, vamos escolher o próprio plano , parametrizado, simplesmente por:
Limitado pelo círculo da fronteira.
Agora é só calcular, vamos ver no que dá!
Passo 6
Temos que calcular a integral do fluxo do rotacional pela nossa superfície , então vamos pela fórmular da definição:
Mas já temos o campo vetorial rotacional e a parametrização, só precisamos encontrar o normal, mas como temos uma parametrização explícita, podemos usar aquele macetinho pra não termos que calcular, ne?
O que facilita muito as coisas. Agora, lembrando que tinhamos encontrado que , então jogando na nossa fórmula:
Mas é o nosso domínio, que vimos que era a circunferência de raio :
Que tem área:
E no final acabou que nem tivemos que fazer integral nenhuma, hein? Quem diria.. haha