Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 821234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 3, lista 3 - 2021.1, Questão 14c

( c ) Calcule ∫ γ F → ⋅ d r → sendo F → = ( - 2 x + y ) i → + ( z 2 c o s ( y ) - y ) j → + ( x 2 + z ) k → e γ a intersecção das superfícies z = x 2 + 2 y 2 e z = y + 1 com projeção no plano x y percorrida uma vez no sentido horário.

Passo 1

Eaew, belezinha?

Precisamos calcular a integral de linha

∫ γ F → ⋅ d r →

tendo o campo vetorial dado por

F → = ( - 2 x + y ) i → + ( z 2 c o s ( y ) - y ) j → + ( x 2 + z ) k →

e a curva sendo a intersecção entre a superfície

z = x 2 + 2 y 2

e, o plano

z = y + 1

Para resolver isso, vamos usar o teorema de Stokes da forma

∫ γ F → ⋅ d r → = ∫ ∫ S ( ∇ → × F → ) ⋅ N →   d S

Ou seja, será que calcular os termos do lado direito da igualdade acima é mais simples do que expandir o lado esquerdo? Vamos checar!

Passo 2

A intersecção será dada pela seguinte elipse

matematicamente podemos obtê-la fazendo

y + 1 = x 2 + 2 y 2

elevando ambos os lados ao quadrado, temos que

y 2 + 2 y + 1 = x 2 + 2 y 2

Ou rearranjando alguns termos

x 2 + y 2 - 2 y = 1

podemos completar quadrado somando 1 2 e subtraindo 1 2 para obter

x 2 + ( y - 1 ) 2 = 2

que na verdade é uma circunferência de raio R = 2 com centro na posição ( x 0 , y 0 ) = ( 0,1 ) . Vamos calcular agora o vetor normal!

Passo 3

Note que precisamos de uma superfície que tenha γ como fronteira, em nosso caso, a superfície mais simples é o próprio plano

f ( x , y ) = z = 1 + y

Precisamos calcular o vetor normal a essa superfície, portanto, iremos considerar a seguinte definição

n → = ∂ ϕ ( u , v ) ∂ u × ∂ ϕ ( u , v ) ∂ v

em que ϕ ( u , v ) é uma parametrização que pode ser escolhida em nosso caso como

ϕ ( u , v ) = ( u , v , 9 - u 2 - v 2 )

Calculando as derivadas parciais, temos que

∂ ϕ ( u , v ) ∂ u = ∂ ∂ u [ ( u , v , 1 + v ] = [ 1,0 , 0 ]

e, da mesma forma, temos que

∂ ϕ ( u , v ) ∂ v = ∂ ∂ v [ ( u , v , 1 + v ] = [ 0,1 , 1 ]

Usando a definição de produto vetorial temos que

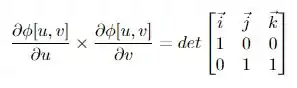
que expandindo o determinante, resulta em

n → = ( 0 - 0,0 - 1,1 - 0 ) = ( 0 , - 1 ,   1 )

Como queremos que o cálculo seja feito no sentido horário, nós iremos considerar na verdade o vetor normal dado por

n → = ( 0,1 , - 1 )

pois ele que indica a circulação horária, pode verificar através da regra da mão direita em nossa figura!Vamos seguir calculando os termos de importância para a nossa integral! Agora, podemos calcular o rotacional!

Passo 4

Beleza, o rotacional do campo é dado por

∇ → × F → = [ ∂ F z ∂ y - ∂ F y ∂ z , ∂ F x ∂ z - ∂ F z ∂ x , ∂ F y ∂ x - ∂ F x ∂ y ]

ou, usando o formato de nosso campo vetorial e calculando as derivadas parciais, temos que

∇ → × F → = [ 0 - 2 z   c o s ( y ) , 0 - 2 x , 0 - 1 ] = ( - 2 z , - 2 x , - 1 )

em termos de nossa parametrização, temos que

∇ → × F → = ( - 2 ( 1 + v ) , - 2 u , - 1 )

A integral toma então a forma

∫ γ F → ⋅ d r → = ∫ ∫ S ( - 2 ( 1 + v ) , - 2 u , - 1 ) ⋅ ( 0,1 , - 1 ) d S

ou, expandindo o produto escalar, temos que

∫ γ F → ⋅ d r → = - 2 ∫ ∫ S u   d S + ∫ ∫ S d S

Para calcular a nossa integral vamos precisar fazer uma mudança de coordenadas! Vamos tentar fazer isso!

Passo 5

Como temos uma esfera, vamos usar coordenadas polares da forma

u = r c o s ( θ )   , v =   r   s e n ( θ )

nesta escolha temos que d S = r   d r d ϕ . Temos o seguinte intervalo 0 ≤ θ ≤ 2 π e o raio está no intervalo 0 ≤ r ≤ 2 , portanto, obtemos

∫ γ F → ⋅ d r → = - 2 ∫ 0 2 ∫ 0 2 π r 2   c o s ( θ )   d r d θ + ∫ 0 2 ∫ 0 2 π r d r d θ

Integrando primeiramente em r , temos que

∫ γ F → ⋅ d r → = - 2 ∫ 0 2 π c o s ( θ ) [ 1 2 + 1 r 2 + 1 ]   | 0 2 d θ + ∫ 0 2 π [ 1 1 + 1 r 1 + 1 ] | 0 2 d θ = - 2 3 [ 2 3 / 2 ] ∫ 0 2 π c o s ( θ ) d θ + ∫ 0 2 π d θ

Resolvendo agora as integrais em θ , temos que

∫ γ F → ⋅ d r → = - 2 3 [ 2 3 / 2 ] [ s e n ( θ ) ] | 0 2 π + [ θ ] | 0 2 π = 2 π

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

∫ γ F → ⋅ d r → = 9 π 5 5

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê