Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 851234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 3, lista 3 - 2021.1, Questão 6a

Calcule

a ∫ ∫ S x z d y ∧ d z + y z d z ∧ d x + x 2 d x ∧ d y , onde S é a semi-esfera x 2 + z 2 + y 2 = a 2   a > 0 ,     z ≥ 0 , orientada segundo a normal exterior;

Passo 1

Eaew, belezinha?

Precisamos calcular a integral de superfície

∫ ∫ S x z d y ∧ d z + y z d z ∧ d x + x 2 d x ∧ d y

Temos que a notação com produto exterior pode ser escrita da seguinte forma:

∫ ∫ S x z d y ∧ d z + y z d z ∧ d x + x 2 d x ∧ d y = ∫ ∫ S x z ( i → ⋅ n → ) d y d x   +   y z ( j → ⋅ n → ) d z   d x   + x 2 ( k → ⋅ n → ) d x d y .

Temos então que:

∫ ∫ S x z d y ∧ d z + y z d z ∧ d x + x 2 d x ∧ d y = ∫ ∫ S F → ( x , y , z ) . n → d S

sendo,

F → ( x , y , z ) = ( x z ,   y z ,   x 2 )

e a superfície considerada é a semi-esfera

x 2 + y 2 + z 2 = a 2 ,   z ≥ 0 .

Para resolver essa integral, vamos parametrizar a superfície e encontrar a sua normal. Vamos lá!

Passo 2

A expressão do vetor normal pode ser obtida através do seguinte produto vetorial

n → = ∂ ϕ ( u , v ) ∂ u × ∂ ϕ ( u , v ) ∂ v

em que ϕ ( u , v ) é uma parametrização da superfície, sendo essa

ϕ ( r , θ ) = ( r c o s θ , r s i n θ , a 2 - r 2   )

em que temos 0 ≤ r ≤ a e 0 ≤ θ ≤ 2 π . O vetor normal pode ser escrito como

n → = ∂ ϕ ( r , θ ) ∂ r × ∂ ϕ ( r , θ ) ∂ θ

Vamos calcular as derivadas e o produto vetorial:

n → = c o s θ ,     s i n θ ,     - r a 2 - r 2   × - r s i n θ ,     r c o s θ ,   0 = ( r 2 c o s θ a 2 - r 2   , r 2 s i n θ a 2 - r 2   , r ) .

Assim, obtemos que a normal é:

  n → = ( r 2 c o s θ a 2 - r 2   , r 2 s i n θ a 2 - r 2   , r )

Antes de ir para a integra, temos temos que escrever a função seguindo a parametrização e também calcular o produto escalar F → . n → .

Passo 3

Vamos escrever a função vetorial F → ( r ,   θ ) :

F → ( x , y , z ) = ( x z ,   y z ,   x 2 ) = ( r c o s θ a 2 - r 2   , r s i n θ a 2 - r 2   , r 2 c o s θ 2 ) .

Então agora podemos calcular o produto escalar:

F → ( x , y , z ) .   n → = ( r c o s θ a 2 - r 2   , r s i n θ a 2 - r 2   , r 2 c o s θ 2 ) . ( r 2 c o s θ a 2 - r 2   , r 2 s i n θ a 2 - r 2   , r )

F → ( x , y , z ) .   n → = ( r 3 c o s θ 2 +   r 3 s i n θ 2 + r 3 c o s θ 2 ) .

Agora precisamos encontrar os limites de integração.

Passo 4

A superfície pode ser representada por essa figura de uma esfera de raio qualquer, lembrando que consideramos   z ≥ 0

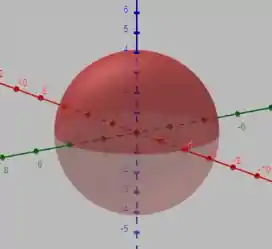
Note que para nossas condições 0 ≤ r ≤ a , que 0 ≤ θ ≤ 2 π . Nossa integral se torna então

∫ ∫ S F → ⋅ n → d S = ∫ 0 a ∫ 0 2 π [ ( r 3 c o s θ 2 +   r 3 s i n θ 2 + r 3 c o s θ 2 ) ] d θ d r

Vamos começar a nossa integração! Saca só!

Passo 5

Podemos começar com qualquer uma das variáveis uma vez que os limites de integração são todos constantes!

∫ ∫ S F → ⋅ n → d S = ∫ 0 a ∫ 0 2 π [ r 3 ( c o s θ 2 + s i n θ 2 ) + r 3 c o s θ 2 ] d θ d r

usando a relação ( c o s θ 2 + s i n θ 2 ) =1 e c o s θ 2 =½ +½ c o s 2 θ , temos que

∫ 0 a ∫ 0 2 π [ r 3 ( c o s θ 2 + s i n θ 2 ) + r 3 c o s θ 2 ] d θ d r = ∫ 0 a ∫ 0 2 π [ r 3 + r 3 ( 1 / 2   + 1 / 2 c o s 2 θ ) ] d θ d r

vamos integrar primeiro em θ , usando então uma série de integrais conhecidas, obtemos o resultado

∫ 0 a ∫ 0 2 π [ r 3 + r 3 ( 1 / 2   + 1 / 2 c o s 2 θ ) ] d θ d r = ∫ 0 a r 3 [ 3 2 θ | 0 2 π - 1 4 [ s i n ( 2 θ ) | 0 2 π ] d r

∫ 0 a r 3 [ 3 2 ( 2 π - 0 ) - 1 4 ( 0 - 0 ) ] d r = ∫ 0 a 3 π r 3 d r

agora integrando em r , usando então uma série de integrais conhecidas, obtemos o resultado

∫ 0 a 3 π r 3 d r = 3 π [ r 4 4 | 0 a ] = 3 π a 4 4 .

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

∫ ∫ S x z d y ∧ d z + y z d z ∧ d x + x 2 d x ∧ d y = 3 π a 4 4

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê