Exercícios Resolvidos de Teorema de Stokes

Ver Teoria

Exercício 36 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

Calcule o fluxo do rotacional do campo através da superfície , com a normal apontando para cima.

Passo 1

“O fluxo do rotacional do campo ”, é muita palavra difícil junta né?

Quando o enunciado pede pra calcularmos um fluxo já sabemos que ele quer a integral de superfície. Nesse caso aqui ao invés de , vamos calcular a integral do rotacional de , ou seja:

É isso! A próxima dificuldade da questão é essa superfície doida aí

Ou seja, só queremos o interior do círculo de raio no plano . Mas como esboçamos isso?

Vamos pensar nos limites superiores disso:

Que é algum valor de negativo, não precisa saber exatamente qual.

E quando :

(Todo número elevado a zero é 1.)

Então quando , temos uma circunferência de raio . Essa é exatamente a nossa fronteira de !

Fizemos essa analise porque na hora da prova a gente não tem um computador pra esboçar a superfície, na verdade ela é essa aqui

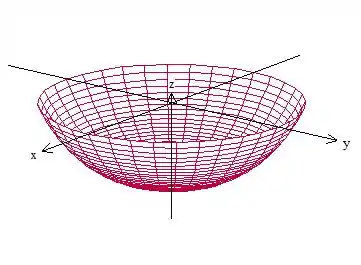
Bom, agora que sabemos qual é a superfície, parece impossível resolver a integral pela definição, não é?

Vamos usar o teorema de Stokes aqui! Ele diz que

Onde

Nesse caso é justamente a circunferência de raio no plano .

Passo 2

Então só precisamos dessa integral de linha aqui

Vamos começar parametrizando a curva, ela está no plano , portanto

Com isso

Passo 3

Pra calcular a integral de linha, ainda precisamos da derivada da parametrização

E também precisamos substituir os parâmetros da curva no campo

Onde

Passo 4

Juntando tudo na integral

Integrando isso aí

Resposta

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k

Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d

Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi

Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .

Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê