Seja a curva a curva dada pela interseção do paraboloide
com o semi-cone
orientada no sentido horário quando observada desde a origem das coordenadas. Calcular
Passo 1
Então, isso aqui é uma integral de linha de um campo vetorial, dado pela função
Então vamos logo de cara calcular o rotacional de .
Bom, o rotacional não é nulo, isso aqui tá cheirando a Teorema de Stokes. Mas o teorema é válido somente para curvas fechadas, então vamos dar uma olhada nessa curva.
Passo 2
Beleza, vamos tentar entender como é a curva .
O paraboloide é centrado no eixo e tem mais ou menos essa cara aqui.
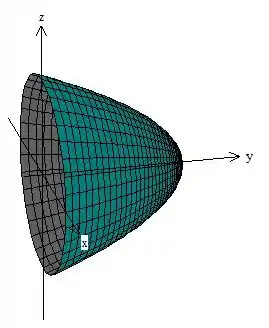
O cone também é centrado no eixo e tem mais ou menos essa cara aqui.
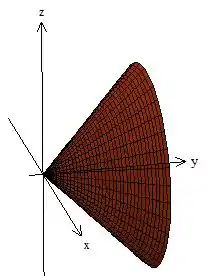
A interseção dos dois é uma curva fechada, alguma coisa com essa cara.
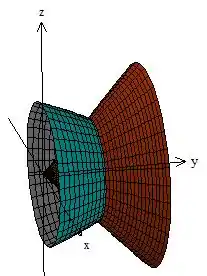
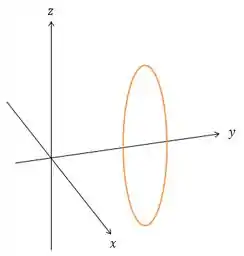
Beleza, então se trata mesmo de uma curva fechada, isso significa que vamos poder aplicar o Teorema de Stokes! :D
Passo 3
O Teorema de Stokes é dado por
Onde vai ser a área da curva.
Já calculamos o antes, agora precisamos ter uma ideia do vetor normal .
O problema falou pra gente que a curva é orientada no sentido horário quando observada desde a origem das coordenadas. Então se estivermos olhando a curva da origem das coordenadas, ela vai ter essa orientação.
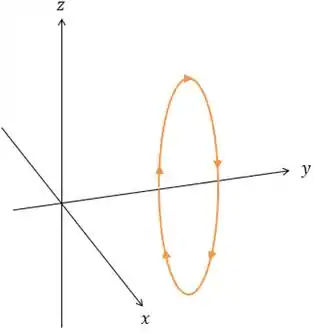
Concorda?
Com essa orientação, o vetor unitário normal a essa superfície com sentido dado pela regra da mão direita seria:
Passo 4
Voltando para o Teorema de Stokes.
Beleza, mas qual a área de ?
Como tanto o paraboloide quanto o cone estão centrados no eixo , podemos usar coordenadas cilíndricas, que nesse caso seriam
Substituindo nas equações do paraboloide e do cone, acharemos
para o paraboloide e
para o cone.
Calculando a interseção entre as duas superfícies, encontraremos:
Como não pode ser negativo, .
Isso quer dizer que corresponde a um círculo de raio no plano .