Exercícios Resolvidos de Teorema de Stokes

Ver Teoria

Exercício 86 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

Use o Teorema de Stokes para calcular

, onde é o triangulo com vértices (1,0,0), (0,1,0) e (0,0,1) orientado no sentido anti-horário quando vista de cima e

Passo 1

Stokes nos diz que:

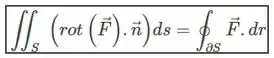
Onde:

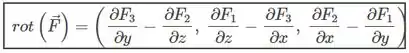
Passo 2

Bom, agora o ideal é a gente encontrar o vetor normal a esse triangulo. Presta atenção nesse passo: Se a gente tem 3 pontos, podemos descobrir dois vetores e com isso calcular o vetor ortogonal ao mesmo tempo aos dois vetores.

Fazendo o vetor

Agora o vetor

Fazendo então o produto vetorial entre eles, descobrindo assim o vetor ortogonal a eles, que também é normal ao plano que estamos procurando.

Passo 3

Agora que nós temos o vetor normal ao plao e pontos contidos nele, a gente consegue descobrir a equação do plano.

Isolando z:

Parametrizando esse plano ficamos com:

Passo 4

Vamos então agora substituir nossa parametrização no pra poder resolver a integral e garantir esse pontinho dessa questão.

Colocando tudo na integral

Isso não é nada mais que a área!

Resposta

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k

Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d

Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi

Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .

Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê