Use o teorema de Stokes para calcular a integral de linha
E que é a curva obtida pela intersecção do cilindro com o plano , orientada no sentido anti-horário quando vista por cima.
Passo 1
A primeira coisa que devemos aqui é entender geometricamente a curva que a gente quer aquela integral de linha.
Então, o próprio problema nos disse que a curva foi obtida através do cilindro e do plano, então vamos desenhar essas duas superfícies juntas e ver essa intersecção acontecer
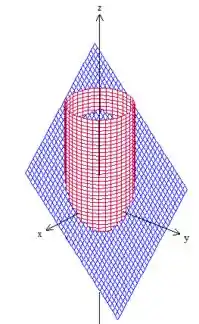
Percebeu? A curva é essa daqui oh
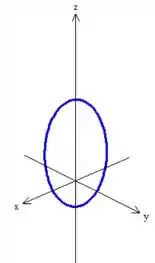
Passo 2
Bem, agora que conhecemos a curva e nos foi dito para fazer utilizando o teorema de , precisamos selecionar uma superfície qualquer que tenha como borda, justamente essa curva.
Quem, podemos escolher?
Sim, o próprio plano azul!
Mas não vamos pegar o plano todo dessa vez, vamos pegar só que está dentro da curva, ou seja, o que está dentro do cilindro, veja só
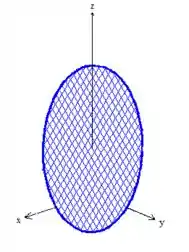
Parametrizar essa superfície não será um grande problema para nós aqui, pois podemos parametrizar como uma parametrização explicita:
Só devemos nos atentar a uma coisinha: Onde estão variando os limites?
Passo 3
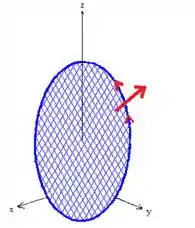
Pois bem, para responder essa pergunta, vamos olhar para a projeção da superfície, no plano .
Olhar para a projeção, é olhar de cima para baixo, dessa forma aqui
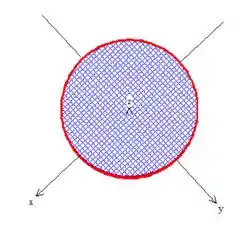
E quando fazemos isso, logo observamos que os nossos parâmetros e de plano que a gente quer, varia dentro do cilindro de raio .
Por uma questão de facilidade, vamos nomear essa região de variação circular de raio do e de .
Passo 4
Bem, agora vamos fazer o que o problema pediu e aplicar o teorema de :
Bem, então basta encontrar esses termos aí e substituir.
Vamos começar pelo rotacional!
Passo 5
Pela fórmula, sabemos que rotacional de um campo é
Onde , e são as coordenadas do campo vetorial que estamos trabalhando, ou seja
Calculando essas derivadas parciais então...
Passo 6
Quanto ao vetor normal, que também necessitamos
E esse vetor normal grandão aí, para encontra-lo, basta jogar na fórmula do bizuzão de quando temos parametrização em forma de uma função explícita , se lembra dela?
Nesse caso, como
Passo 7
Não podemos deixar de checar se estamos com o vetor normal correto, heim!
Mas para fazer isso, basta seguir o que o problema nos pediu, ou seja, a rotação na curva deve estar no sentido anti-horário quando vista de cima:
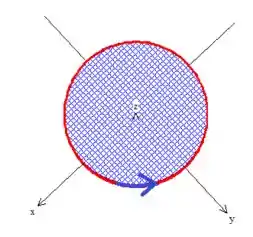
Pela regra mão direita, concluímos que o vetor normal deve
Ter coordenada , positiva. Logo... Estamos com o vetor correto !
Passo 8
Voltando para o teorema de substituindo os caras que já determinamos
Calculando esse produto interno aí
Passando tirando esse da integral...
Epa! Quem é essa integral aí? É a área da região ! :D
Como a região é
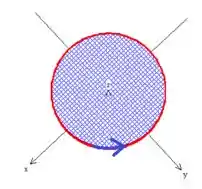
um circulo de raio 1, sua área será , logo