Calcule a integral de superfície , em que
E é a parte do plano dentro do cilindro , com orientação para cima.
Passo 1
Antes de tudo vamos fazer um gráfico da região para entender melhor a questão. Temos o plano dentro do cilindro , o que nos dá isso aqui:
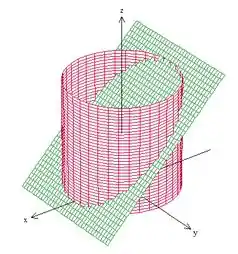
Como a equação do plano não possui a coordenada , quer dizer que esse plano é paralelo ao eixo . Então, para desenhá-lo, basta você fazer a reta no plano e “repetí-la” ao longo do eixo , desenhando traços paralelos a ela.
A questão pede para calcularmos a integral de superfície em , que é a parte do plano verde que está dentro do cilindro. Como podemos ver, essa superfície é uma elipse inclinada.
Passo 2
Como o problema pede
Precisamos, então, calcular , sabendo que
Temos:
Passo 3
Agora vamos parametrizar a superfície .
Temos uma elipse pertencente ao plano . Para parametrizar esse plano, vamos isolar a variável e usar e como parâmetros:
Agora para descobrimos os intervalos de e , para descrever o domínio dessa função no plano . Para isso, precisamos imaginar a superfície vista de cima, no caso, temos um círculo de raio :
Isso porque quem limita o plano é o cilindro.
Portanto, nossa superfíce é parametrizada por
Satisfazendo a condição
Passo 4
Calcular
Como o problema diz que a normal aponta para cima e encontramos para esse vetor normal, sabemos que encontramos o vetor certo.
Passo 5
Agora vamos montar a integral:
Onde é a projeção da nossa superfíce no plano , que já vimos que é o círculo
Esse é o limite da parametrização do plano. Temos:
Agora calma! Antes de sairmos calculando, vamos pensar um pouco aqui. A integral dupla de em não nos dá a área de ? E não é um círculo de raio ? Olha só o que podemos fazer então:
Isso porque sabemos que a área do círculo é .