Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 441234567891011121314151617181920212223242526272829303132333435363738394041424345464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Use o teorema de Stokes para calcular a integral ∬ S   r o t   F ∙ d S , em que

F x ,   y ,   z = z i + x j + y k ,

E S é o hemisfério x 2 + y 2 + z 2 = 1 , z ≥ 0 , orientada para cima.

Passo 1

Não podemos deixar de começar um exercício de S t o k e s como esse sem ver quem é essa superfície, certo?

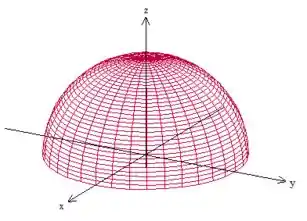
Bem, a sorte aqui é que a superfície é uma velha conhecida nossa! É a semiesfera de raio 1 , bem eu digo semi, pois só queremos a parte onde z é positivo, ou seja:

Passo 2

Vamos fazer algumas observações a respeito dessa superfície aí:

Para começar ela é uma superfície aberta tendo como borda, justamente a o plano z = 0 . Graficamente, podemos ver essa borda, e ela é uma circunferência

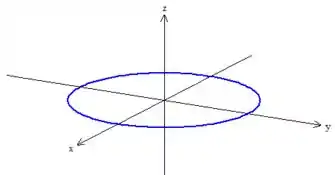
Pra equação dela, como sabemos que essa curva está no plano z = 0 , basta substituir na equação da semiesfera

x 2 + y 2 + z 2 = 1       →             x 2 + y 2 + 0 2 = 1

x 2 + y 2 = 1

A segunda observação a se fazer é com relação a orientação:

Como temos que o vetor normal à superfície está saindo dela

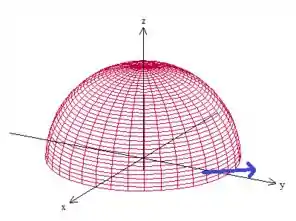
Portanto pela regra da mão direita, podemos definir o sentido de giro da borda, ou seja, ele gira no sentido anti-horário quando vista de cima:

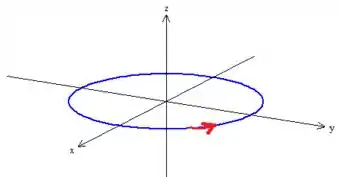
Passo 3

Graças a essas observações importantíssimas a gente pode prosseguir e chamar o nosso amigo S t o k e s , pois se a gente tem uma superfície fechada com borda uma curva fechada e orientada positivamente (por isso a análise de giro da curva), então

∬ S   r o t   F ∙ d S = ∫ C   F ∙ d r →

Onde essa curva C aí é justamente a curva que temos.

Bem, antes de calcular essa integral de linha aí e resolver o nosso problema, devemos parametrizar essa curva. Bora?

Passo 4

Bem, aqui exige muita atenção!

Qual é uma ótima parametrização para essa curva que atende essa condição de giro (no sentido anti-horário)?

Bem, por ser uma circunferência, com certeza a gente vai parametrizar comparando com aquela equação da trigonometria, se lembra?

sin 2 ⁡ θ + cos 2 ⁡ θ = 1             ⇒ C o m p a r a n d o …             x 2 + y 2 = 1

Bem então a gente tende a pegar naturalmente

x = cos ⁡ θ

y = sin ⁡ θ

Nota que essa parametrização atende o giro, porque quando vamos aumentando o θ que sai do z e r o , o y vai aumentando e o x diminuindo, exatamente o que queremos percebeu?

Não podemos esquecer que essa curva está no espeço, e, portanto tem a coordenada z , que nesse caso é z = 0 , hehe! (ela está em cima do plano z = 0 )

Logo, a parametrização ficou

γ θ = cos ⁡ θ , sin ⁡ θ ,   0

Como a gente dá uma volta completa...

0 ≤ θ ≤ 2 π

Passo 5

Para resolver aquela integral de linha do teorema de S t o k e s , não podemos esquecer-nos de calcular o d r → .

A gente sabe que esse termo é

  d r → = γ ' θ d θ

Derivando então a curva

γ ' θ = - sin ⁡ θ , cos ⁡ θ ,   0

Ou seja d r → = - sin ⁡ θ , cos ⁡ θ ,   0 d θ

Passo 6

Voltando para a integral de linha que devemos resolver e dessa vez substituindo tudo, a gente tem

∫ C   F ∙ d r → = ∫ 0 2 π z ,   x ,   y ∙ - sin ⁡ θ , cos ⁡ θ ,   0 d θ

Como estamos integrando em θ , devemos sumir com essas coordenadas antigas aí.

Podemos fazer isso substituindo pelas variáveis novas, sacou?

∫ 0 2 π 0 , cos ⁡ θ , sin ⁡ θ ∙ - sin ⁡ θ , cos ⁡ θ ,   0 d θ

Resolvendo esse produto interno aí

∫ 0 2 π cos 2 ⁡ θ d θ

Como

∬ S   r o t   F ∙ d S = ∫ C   F ∙ d r → = ∫ 0 2 π cos 2 ⁡ θ d θ

Basta resolver essa integral aí e tá tido certo!

Passo 7

Bem, agora, para resolver essa integral aí, devemos recordar que podemos substituir esse cosseno aí por cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2 .

∫ 0 2 π cos 2 ⁡ θ d θ = ∫ 0 2 π 1 + cos ⁡ 2 θ 2 d θ =

1 2 ∫ d θ + ∫ cos ⁡ 2 θ d θ 0 2 π

A primeira integral a gente já mata

1 2 θ + ∫ cos ⁡ 2 θ d θ 0 2 π

Quanto a segunda, matamos também, basta fazer uma mudança 2 θ = a

d a = 2 d θ         →               d θ = d a 2

1 2 θ + ∫ cos ⁡ a d a 2 0 2 π = 1 2 θ + 1 2 sin ⁡ a 0 2 π

Não esqueça de voltar com a variável θ heim!

1 2 θ + 1 2 sin ⁡ 2 θ 0 2 π =

Substituindo lembrando que sin ⁡ 4 θ = sin ⁡ 2 θ = sin ⁡ 0 = 0

1 2 2 π =

π

Resposta

∬ S   r o t   F ∙ d S = π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê