Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 541234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Teorema de Stokes

Seja F x , y , z = cos ⁡ ( z ) + x y 2 i + x e - z   j + s e n y + x 2 z k .

  1. Seja I = ��� S   ( ∇ × F ) . d S , onde S é a superfície do paraboloide z = x 2 + y 2 limitado pelo plano z = 4 , com vetores normais apontando para fora. Mostre que I = - 4 π e 4 , usando:

b2) o Teorema de Stokes, calculando uma integral de linha.

Passo 1

Precisamos mostrar que:

I = ∬ S   r o t F → . d S = - 4 π e 4

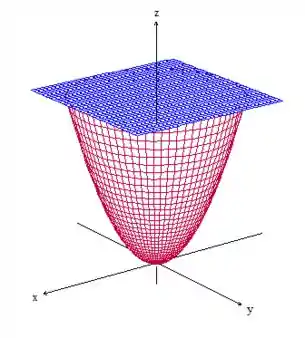
Onde S é o paraboloide z = x 2 + y 2 cortado pelo plano z = 4 .

Passo 2

Aplicando o Teorema de Stokes, podemos trocar uma integral de superfície por uma integral de linha na sua borda. Aplicando ao problema, podemos escrever:

∮ C   F → . d r = ∬ S   r o t F → . d s = I

Sacou? Ou seja, precisamos calcular apenas a integral de linha de F na fronteira de S , no caso, uma circunferência.

Passo 3

Para achar a equação dessa circunferência, basta fazer z = 4 na equação do paraboloide:

z = x 2 + y 2 = 4

Logo, temos uma circunferência de raio 2 em z = 4 . Podemos parametrizar em coordenadas polares com r = 2 :

σ θ = 2 cos ⁡ θ ,   2   s e n   θ , 4

Agora vamos pensar: S está orientada com vetores normais apontando para fora, não é? Pela Regra da Mão Direita, para a borda estar orientada positivamente, deve girar no sentido horário então.

Logo, θ vai de 2 π a 0 . Foi? Agora precisamos derivar essa parametrização:

σ θ = - 2   s e n   θ ,   2 cos ⁡ θ , 0

Passo 4

Agora, vamos trazer tudo para a fórmula da integral de linha:

I = ∫ C   F x , y , z ⋅ d r = ∫ a b F x t ,   y t ,   z ( t ) ⋅ r → ' t d t

Escrevendo o campo em função da parametrização:

F x , y , z = cos ⁡ ( z ) + x y 2 i + x e - z   j + s e n y + x 2 z k

F σ θ = cos ⁡ 4 + 8 cos ⁡ θ s e n 2 θ , 2 cos ⁡ θ e - 4 , ?

Não escrevemos a última componente porque ela vai desaparecer no produto vetorial!

Isso nos dá:

I = ∫ 2 π 0 cos ⁡ 4 + 8 cos ⁡ θ s e n 2 θ , 2 cos ⁡ θ e - 4 , ? . - 2   s e n   θ ,   2 cos ⁡ θ , 0 d θ

= ∫ 2 π 0 - 2   s e n   θ cos ⁡ 4 - 16 cos ⁡ θ s e n 3 θ + 4 cos 2 ⁡ θ e - 4 d θ =

Lembrando que

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

Temos:

= ∫ 2 π 0 - 2   s e n   θ cos ⁡ 4 - 16 cos ⁡ θ s e n 3 θ + 2 e - 4 ( 1 + cos ⁡ 2 θ ) d θ =

= ∫ 2 π 0 - 2   s e n   θ cos ⁡ 4 - 16 cos ⁡ θ s e n 3 θ + 2 e - 4 + 2 e - 4 cos ⁡ 2 θ d θ =

Agora é só resolver isso aí:

= 2 cos ⁡ θ cos ⁡ 4 + 4   s e n 4 θ + 2 e - 4 θ + e - 4 s e n   2 θ 2 π 0 =

= - 4 π e 4

Pronto, chegamos ao resultado!

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê