Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 381234567891011121314151617181920212223242526272829303132333435363739404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Seja S a superfície z = 2 x y e C a interseção desta superfície com o cilindro x 2 + y 2 = 1 (com orientação no sentido anti-horário – quando vista de cima). Calcule (através do Teorema de Stokes) a integral

∮ C F → ⋅ d r → ,

onde

F → = e x cos ⁡ x 4   i ^ + x   j ^ - x y   k ^ .

Passo 1

Cara, ele falou para gente usar o teorema de Stokes. Bora começar pelo cálculo do rotacional desse campo então:

Ele tem essa fórmulinha:

r o t   F → = i ^ j ^ k ^ ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3

Nosso campo é:

F → = ( e x cos ⁡ x 4   i ^ + x   j ^ - x y   k ^ .

F → = F 1 , F 2 , F 3 = ( e x cos ⁡ x 4 , x , -   x y )

Então precisamos calcular:

r o t   F → = i ^ j ^ k ^ ∂ ∂ x ∂ ∂ y ∂ ∂ z e x cos ⁡ x 4 x - x y

r o t   F → = ∂ - x y ∂ y - ∂ x ∂ z i ^ - ∂ - x y ∂ x - ∂ e x cos ⁡ x 4 ∂ z j ^ + ∂ x ∂ x - ∂ e x cos ⁡ x 4 ∂ y k ^

r o t   F → = ( - x - 0 ) i ^ - - y - 0 j ^ + 1 - 0 k ^

r o t   F → = - x , y ,   1

Prontinho. Vem comigo!

Passo 2

O Teorema de Stokes diz que:

∫ δ S F → ⋅ d r → = ∫ ∫ S r o t   F ⋅ n → d s

δ S é a nossa curva C . Ela precisa ser a fronteira de uma superfície. A nossa curva é a interseção de z = 2 x y com um cilindro. Então a gente pode escolher uma dessas superfícies. A mais fácil de usar é z = 2 x y . Então vamos dizer que S é:

z = 2 x y

Dentro do cilindro x 2 + y 2 = 1 . E aí a gente pode escrever:

x 2 + y 2 ≤ 1

Aí a gente reescreve nossa equação assim:

∫ C F → ⋅ d r → = ∫ ∫ S r o t   F → ⋅ n → d s

Então a ideia é que a gente só precisa montar e calcular a integral da direita, para então achar o valor da esquerda. Maneiro, né?

Passo 3

Maaas a gente precisa atender a alguns critérios para podermos aplicar esse teorema antes de começar:

1. Nossa fronteira precisa estar orientada positivamente em relação a superfície. Ele diz que nossa curva está sendo percorrida no sentido anti-horário.

Ao percorrer essa curva e olharmos para a esquerda, precisamos estar vendo a superfície que limitamos (a z = 2 x y dentro do cilindro). E isso acontece na nossa situação. Então tá beleza.

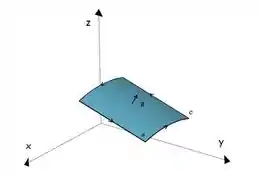
E já que estamos no sentido anti-horário, e temos uma fronteira exterior a superfície, nosso vetor normal a superfície precisa estar orientado para cima (componente z ≥ 0 ). Tipo nesse caso genérico. Vemos isso pela regra da mão direita.

2. O campo e suas derivadas precisam estar bem definidos para o domínio de integração. Olha ele:

F → = ( e x cos ⁡ x 4   i ^ + x   j ^ - x y   k ^

Não tem nenhum ponto de descontinuidade aí né (nenhum denominador que possa zerar ou algo assim). Não vai aparecer isso nas derivadas dessas funções também.

Então a gente pode confiar que ele está bem definido para o nosso domínio de integração, já que ele está bem definido para todos os valores de x , y , z .

Então, tá belezinha, a gente pode usar o teorema sem preocupações. Bora lá!

Passo 4

Vamos começar parametrizando z = 2 x y dentro do cilindro, porque estamos montando uma integral de superfície. Como ela pode ser escrita como uma função de x e y explícita:

z = f x , y = 2 x y

A gente pode parametrizar ele assim:

φ x , y = x , y , f x , y

φ x , y = x , y , 2 x y

E ele diz que nossa superfície está dentro do cilindro, aí a gente pode escrever que nosso domínio é:

D :   x 2 + y 2 ≤ 1

Como esse é o domínio da parametrização, também será o domínio da nossa integral.

Passo 5

Depois a gente precisa calcular nosso vetor normal. Quando a gente usa essa parametrização aí de cima, o vetor normal é mais tranquilo de achar. Ele tem essa cara:

n → = ∂ φ ∂ x × ∂ φ ∂ y = - ∂ f ∂ x ,   - ∂ f ∂ y , 1

Aí para o nosso caso:

z = f x , y = 2 x y

n → = ∂ φ ∂ x × ∂ φ ∂ y = - 2 y ,   - 2 x , 1

Repara que a componente z do nosso vetor é sempre positiva, então ele está virado para cima como queremos.

Passo 6

Nossa integral ficou assim:

∫ C F → ⋅ d r → = ∫ ∫ S r o t   F → ⋅ n → d s = ∫ ∫ x 2 + y 2 ≤ 1 - x , y ,   1 ⋅ - 2 y ,   - 2 x , 1 d x d y

∫ C F → ⋅ d r → = ∫ ∫ x 2 + y 2 ≤ 1 2 x y - 2 x y + 1 d x d y = ∫ ∫ x 2 + y 2 ≤ 1 1 d x d y

A integral dupla sobre esse círculo de raio 1 vai ser igual a área do círculo! Isso porque o argumento dela é 1 . Como a área do círculo é π r 2 e r = 1 :

∫ C F → ⋅ d r → = π

Prontinho!

Resposta

∮ C F → ⋅ d r → = π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê