Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 311234567891011121314151617181920212223242526272829303233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 14) Seja S a calota esférica dada pela equação x 2 + y 2 + z 2 = 4 , onde 0 ≤ z ≤ 2 . Sobre S fixe a orientação n → tal que n → 0 ,   0 ,   2 = k → . Calcule

∬ S   r o t   F → ⋅ n →   d S

Onde F → x ,   y ,   z = - y 3 3 + z   e x , x 3 3 - cos ⁡ y z ,   x y

Passo 1

Bem, vamos com calma aqui. Queremos calcular:

∬ S   r o t   F → ⋅ n →   d S

Em cima de S que nos representa uma “calota”:

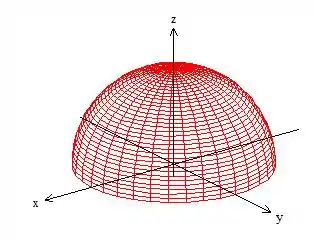
Veja que a calota é uma na realidade a parte de cima da esfera de raio 2 .

Essa integral de superfície é típica de problema de Stokes e é justamente ele que vamos tentar utilizar aqui, já que de acordo com esse Teorema, podemos aplicar

∬ S   r o t   F → ⋅ n →   d S = ∫ ∂ S   F → ⋅ d r →

Onde essa integral de linha é calculada na borda de S , ou seja, em cima dessa curvinha azul aí:

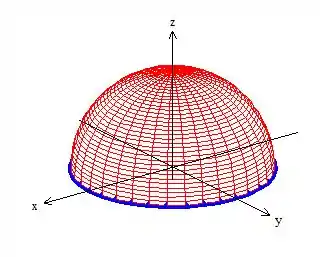
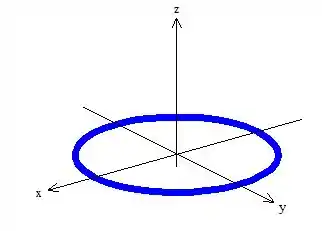
Não sei você, mas eu não quero calcular a integral de linha em cima dessa circunferência aí não! Ora, vai dar mais trabalho! Então o que acha de tentar voltar pra integral de superfície?

Passo 2

Sim, vamos retornar a integral de superfície, mas não pra aquela dali em S :

∬ S   r o t   F → ⋅ n →   d S

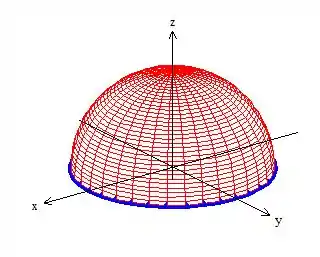
O teorema de Stokes é legal com a gente. Ele fala que se pode calcular a integral de superfície em qualquer superfície desde que a superfície escolhida tenha como borda a curva que eu te mostrei. Ora, e qual superfície, além de S , que tem como borda esse cara? O próprio círculo em cima do plano z = 0 ! :D

Então, chamando esse plano de superfície 2 , S 2 , pelo teorema de Stokes...

∫ ∂ S   F → ⋅ d r → = ∬ S 2   r o t   F → ⋅ n →   d S

Logo...

∬ S   r o t   F → ⋅ n →   d S = ∬ S 2   r o t   F → ⋅ n →   d S

Veja que ironia nessa última igualdade. Nós queríamos calcular uma integral de superfície em cima de uma superfície que não continha o círculo, mas por Stokes calcular a integral em cima dessa calota é o mesmo que calcular em cima do círculo!

Doideira, neh? Então bora comigo calcular essa integral em S 2 :D

Passo 3

Primeiro quem é o rotacional?

r o t   F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y →

Como

F → x ,   y ,   z = - y 3 3 + z   e x , x 3 3 - cos ⁡ y z ,   x y = F 1 ,   F 2 ,   F 3

Então, pelo cálculo das derivadas parciais...

r o t   F → = x - sin ⁡ y z ⋅ y , e x - y , x 2 - - y 2   →

r o t   F → = x - y sin ⁡ y z , e x - y , x 2 + y 2  

Logo, vamos ter que calcular a integral de superfície desse vetor aí! Fique atento para não esquecer e usar F → , heim!

Passo 4

Tá, agora quem é a superfície S 2 ? Ora é o círculo no plano x y , neh:

Veja que esse plano tem o vetorsinho normal n → apontando justamente pra cima, logo ele tem coordenadas:

n → = 0 ,   0 ,   1

Esse vetor é justamente o vetor pedido no problema, já que ele aponta pra cima, logo...

∬ S 2   r o t   F → ⋅ n →   d S = ∬ S 2   x - y sin ⁡ y z , e x - y , x 2 + y 2   ⋅ 0 ,   0 ,   1   d S =

∬ S 2   x 2 + y 2   d S

Passo 5

Precisamos da superfície S 2 parametrizado para prosseguir com os cálculos:

Como é um círculo, podemos parametrizar utilizando coordenadas cilíndricas...

x = r cos ⁡ θ

y = r sin ⁡ θ

Como o z do círculo é conhecido (ele está em cima do plano x y )...

z = 0

Então a gente pode em uma notação mais elegante, falar que a parametrização é...

σ r ,   θ = r cos ⁡ θ ,   r sin ⁡ θ ,   0

Onde r e θ varia com o círculo. θ podemos afirmar de antemão que ele dá uma volta completa, logo...

0 ≤ θ ≤ 2 π

Já o raio, depende do raio do círculo. Bem, podemos encontra esse raio fazendo o z = 0 na equação da esfera...

x 2 + y 2 + z 2 = 4           →                 x 2 + y 2 = 4

Ou seja, é um círculo de raio 2 , logo, o raio r varia de 0 até esse cara, veja...

0 ≤ r ≤ 2

Passo 6

O termo d S dessa parametrização é...

d S = N → d r d θ

Onde

N → = ∂ σ r ,   θ ∂ r × ∂ σ r ,   θ ∂ ��

σ r ,   θ = r cos ⁡ θ ,   r sin ⁡ θ ,   0             →               ∂ σ r ,   θ ∂ r = cos ⁡ θ ,   sin ⁡ θ ,   0

σ r ,   θ = r cos ⁡ θ ,   r sin ⁡ θ ,   0             →               ∂ σ r ,   θ ∂ θ = - r sin ⁡ θ ,   r cos ⁡ θ ,   0

N → = i → j → k → cos ⁡ θ sin ⁡ θ 0 - r sin ⁡ θ   r cos ⁡ θ 0       →

N → = r cos 2 ⁡ θ k → - - r sin 2 ⁡ θ k →   →

N → = r cos 2 ⁡ θ + sin 2 ⁡ θ k → →

N → = r k →

Logo...

N → = r 2 = r

Passo 7

Voltando para a integral que precisamos resolver...

∬ S 2   x 2 + y 2   d S     →

Colocando esse x 2 + y 2 em coordenadas cilíndricas...

∬ S 2   r cos ⁡ θ 2 + r sin ⁡ θ 2   d S   →

∬ S 2   r 2 cos 2 ⁡ θ + sin 2 ⁡ θ   d S   →

∬ S 2   r 2   d S   →

Agora trocando o S 2 pelas variações de r e θ enquanto que o d S ...

∫ 0 2 π ∫ 0 2 r 3 d r d θ

Agora é só resolver essa integral e correr para o abraço 😉!

Passo 8

∫ 0 2 π ∫ 0 2 r 3 d r d θ = ∫ 0 2 π ∫ 0 2 r 3 d r d θ =

∫ 0 2 π r 4 4 0 2 d θ = 4 ∫ 0 2 π d θ =

8 π

Passo 9

Veja bem, encontramos o valor da integral em S 2 . Mas como vimos...

∬ S   r o t   F → ⋅ n →   d S = ∬ S 2   r o t   F → ⋅ n →   d S

Então

∬ S   r o t   F → ⋅ n →   d S = 8 π

Resposta

8 π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê