Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 591234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575860616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFMG, Sem Campus, Cálculo 3, P3 - 2021.2, Questão 1.

Seja F x , y , z = z - y + e x 2 i + x - z + e y 2 j + y - x + e z 2 k e seja γ o triângulo de vértices A = 1,0 , 0 , B = 0,1 , 1 e C = 0,0 , 1 orientado no sentido tal que C segue A e precede B . Calcule ∫ γ F d r .

a) 1

b) - 2

c) 0

d) 2

e) - 1

Passo 1

Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nesse problema, estamos interessado em obter a integral ∫ γ F d r em que F x , y , z = z - y + e x 2 i + x - z + e y 2 j + y - x + e z 2 k e γ é um triangulo cujos vértices é dado por A = 1,0 , 0 , B = 0,1 , 1 e C = 0,0 , 1 orientado na ordem A B C , ou seja, no sentido anti-horário.

Como podemos fazer isso? 🤔

Para obter essa integral, vamos aplicar o teorema de Stokes, esse teorema consiste em calcular a integral do campo vetorial como

∫ γ F d r = ∬ S r o t F → · n → d S

Em que

r o t ( F → ) = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

E n → é um vetor normal unitário à superfície.

Sacou? Bora lá! 😁

Passo 2

Vamos começar obtendo o r o t ( F → )

r o t ( F → ) = ∂ y - x + e z 2 ∂ y - ∂ x - z + e y 2 ∂ z ,   ∂ z - y + e x 2 ∂ z - ∂ y - x + e z 2 ∂ x ,   ∂ x - z + e y 2 ∂ x - ∂ z - y + e x 2 ∂ y

r o t ( F → ) = 1 - - 1 ,   1 - - 1 ,   1 - - 1

r o t ( F → ) = 2,2 , 2

Já para obter o vetor normal à superfície, vamos primeiro visualizar a superfície...

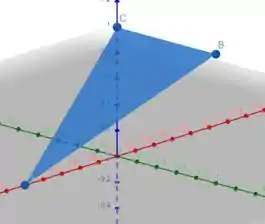
Podemos obter o vetor normal à superfície percebendo que se trata de um plano x + z = 1 , ou seja

n → = - 1,0 , 1 2

Substituindo no teorema, vamos obter

∫ γ F d r = ∬ S 2,2 , 2 · - 1,0 , 1 2 d S

∫ γ F d r = ∬ S - 2 2 - 2 2 d S

∫ γ F d r = ∬ S - 4 2 d S

Legal, né? 😎

Passo 3

Como - 4 2 é uma constante podemos tirar da integral

∫ γ F d r = - 4 2 ∬ S d S

Uma integral dupla de uma superfície nada mais é que a área dessa superfície, ou seja ∬ S d S é a área do triângulo!

Analisando a imagem, vemos que a base é b = 1 e a altura é obtida aplicando Pitágoras no triangulo que é formado em y = 0

h = 1 2 + 1 2 = 2

Logo

∬ S d S = b · h 2 = 1 · 2 2

∬ S d S = 2 2

Substituindo em Stokes, temos

∫ γ F d r = - 4 2 2 2

∫ γ F d r = - 2

Fim! Iae, o que achou? Responde Aí! 😁

Resposta

b) - 2

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê