Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 471234567891011121314151617181920212223242526272829303132333435363738394041424344454648495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 3: Utilize o Teorema de Stokes para calcular a integral de linha

∫ γ   2 x e y + z x   d x + x 2 e y + y 3 d y + y + ln ⁡ z 4 + 1 d z

Onde γ é a curva parametrizada por σ t = 2 cos ⁡ t ,   3 sin ⁡ t , cos ⁡ t + sin ⁡ t ,   t ∈ 0 ,   2 π .

Passo 1

Antes de começarmos o nosso problema em si, vamos fazer uma pequena mudança: particularmente acho além de feio, confuso, aquela notação de integral de linha ali no enunciado, então vamos mudar:

∫ γ   2 x e y + z x   d x + x 2 e y + y 3 d y + y + ln ⁡ z 4 + 1 d z = ∫ γ   F → ⋅ d r →

Essa então é a integral de linha que queremos resolver, onde o campo vetorial F → é...

F → = 2 x e y + z x ,   x 2 e y + y 3 ,   y + ln ⁡ z 4 + 1

Não se preocupe com o que acabamos de fazer, foi apenas escrever a integral de linha de uma forma mais elegante ! Porém, isso não é tão importante assim, pois o que queremos fazer mesmo é resolvê-la aplicando o Teorema de Stokes:

∫ ∂ S   F → ⋅ d r → = ∬ S   r o t F → ⋅ n →   d S

Passo 2

Como deu para perceber, essa última igualdade (do Teorema de Stokes), envolve uma integral de superfície, e nem sempre resolvê-la é mais fácil do que calcular uma integral de linha. Nesse caso vai ser, pois o problema já nos mandou fazer assim, mas se ele não nos tivesse pedido, bastava calcular esse rotacional e vê se ele simplifica as contas:

r o t   F = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Onde F 1 , F 2 e F 3 são as componentes do campo F ...

F = F 1 ,   F 2 ,   F 3 = 2 x e y + z x ,   x 2 e y + y 3 ,   y + ln ⁡ z 4 + 1

Calculando essas derivadas parciais:

r o t   F = 1 - 0 ,   x - 0 ,   2 x e y - 2 x e y

r o t   F = 1 ,   x ,   0

Veja que esse rotacional é relativamente mais bonito de simples que o próprio campo, e isso nos sugere Stokes, mesmo que o problema não nos falasse nada, saca?

Passo 3

O Teorema de Stokes, como já vimos, é a maravilhosa igualdade entre uma integral de linha e uma integral de superfície:

∫ C   F ⋅ d r → = ∬ S   r o t   F ⋅ n →   d S

Mas calma lá, jovem! Antes de aplicarmos o teorema em si, devemos verificar se estamos nas condições que o Teorema nos exige:

  1. Ter uma curva C fechada delimitando a superfície S .
  2. Um campo sem singularidades.
  3. E por último, ter uma orientação positiva.

Nos próximos três passos, vamos avaliar cada um deles, ok?

Passo 4

1 )

Quanto a primeira exigência, bem... Precisamos de uma curva fechada. O que nos remete a uma pergunta: Será que a nossa curva é fechada? Vejamos o que o problema nos disse:

“... onde γ é a curva parametrizada por

σ t = 2 cos ⁡ t ,   3 sin ⁡ t , cos ⁡ t + sin ⁡ t ,   t ∈ 0 ,   2 π .”

Show! Veja então que se a gente “desparametrizar a curva”, ou seja, voltar para as coordenadas cartesianas, obteremos:

x = 2 cos ⁡ t

y = 3 sin ⁡ t

z = cos ⁡ t + sin ⁡ t

Com as duas primeiras equações...

cos ⁡ t = x 2           e           sin ⁡ t = y 3

Como cos 2 ⁡ t + sin 2 ⁡ t = 1 , pela equação fundamental da trigonometria...

x 2 4 + y 2 9 = 1

Que nos representa um cilindro (já dava até para desconfiar, pois aquela parametrização é a cara de uma parametrização em coordenadas cilíndricas).

Mas com a terceira equação...

z = cos ⁡ t + sin ⁡ t     →

z = x 2 + y 3         →          

6 z = 3 x + 2 y

E essa nos representa um plano! Então a nossa curva é a intersecção do cilindro com o plano! :

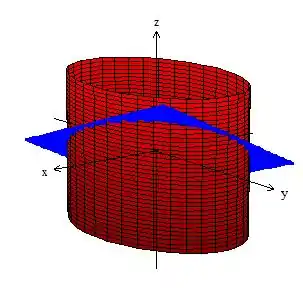
E como ela foi parametrizada dessa forma aqui σ t = 2 cos ⁡ t ,   3 sin ⁡ t , cos ⁡ t + sin ⁡ t ,   t ∈ 0 ,   2 π , com t girando de 0 a 2 π , ainda podemos falar que essa curva gira no sentido anti-horário quando vista de cima:

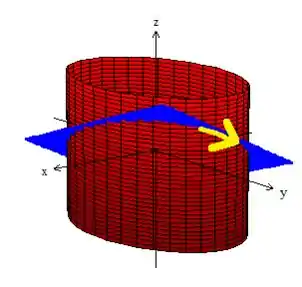
Concluímos então que a curva é sim FECHADA, e mais, ela delimita uma superfície circular de plano em cima dela, a qual vamos chamar de S (superfície do plano azul).

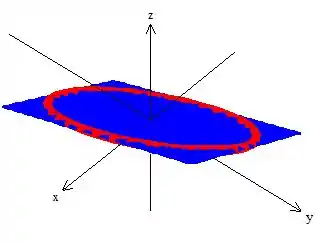
Passo 5

2 )

A outra preocupação de Green se refere ao campo F → . De acordo com ele, temos que ter um campo sem singularidades onde estamos trabalhando, ou seja, sem problemas de definição:

F → = 2 x e y + z x ,   x 2 e y + y 3 ,   y + ln ⁡ z 4 + 1

E veja que o nosso não tem nenhum!

Passo 6

3 )

Por último, temos que ter uma orientação positiva entre sentido de giro da curva e o sentido do vetor normal à superfície.

Como a nossa curva gira no sentido anti-horário, aplicando a regra da mão direita, verificamos que o vetor normal só pode estar pra cima:

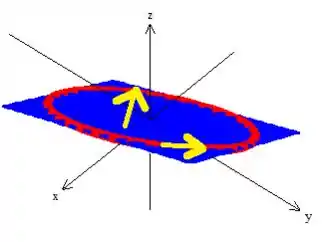
Passo 7

Com tudo isso sendo satisfeito, podemos finalmente retornar ao problema e aplicar S t o k e s sem medo de ser feliz:

∫ ∂ S   F ⋅ d r → = ∬ S   r o t   F ⋅ n →   d S

Como a borda da superfície S ∂ S é a curva γ ...

∫ γ   F ⋅ d r → = ∬ S   r o t   F ⋅ n →   d S

Bora calcular essa integral de superfície e matar o problema então?

Passo 8

∬ S   r o t   F ⋅ n →   d S

Primeiro devemos parametrizar a superfície S ! Como é um pedaço de plano com uma equação explícita...

6 z = 3 x + 2 y     →

z = 3 x + 2 y 6

Podemos parametrizar explicitamente com os dois parâmetros sendo o x e o y , no caso:

φ x ,   y = x ,   y ,   3 x + 2 y 6

Com o x e o y variando dentro do cilindro...

x 2 4 + y 2 9 ≤ 1

Passo 9

Agora... Precisamos do termo n → d S :

n → d S = N →   d x d y

Como a parametrização foi feita em termos de uma função de x e y , podemos usar o Bizu de Vetor normal:

N → = - ∂ z ∂ x ,   - ∂ z ∂ y ,   1   →           j á   q u e       z = 3 x + 2 y 6

N → = - 1 2 ,   - 1 3 ,   1

Veja que esse é justamente o vetor normal que buscamos, afinal de contas ele tem a entrada z positiva (apontando pra cima). Portanto:

n → d S = - 1 2 ,   - 1 3 ,   1   d x d y

Passo 10

Com tudo isso, podemos regressar a integral de superfície...

∬ S   r o t   F ⋅ n →   d S

Onde vamos substituir tudo...

∬ S   r o t   F ⋅ n →   d S = ∬ D   1 ,   x ,   0 ⋅ - 1 2 ,   - 1 3 ,   1   d x   d y =

∬ D   - 1 2 - x 3   d x   d y

Veja que agora temos que resolver uma integral dupla, onde a região D esta dentro de uma elipse:

x 2 4 + y 2 9 ≤ 1

Podemos então utilizar as coordenadas elípticas:

x = 2 r cos ⁡ θ

y = 3 r sin ⁡ θ

J = 2 ⋅ 3 ⋅ r

Com o r variando de 0 a 1 e o θ dando uma volta completa (de 0 a 2 π ).

Assim:

∬ D   - 1 2 - x 3   d x   d y = ∬ D   - 1 2 - 2 r cos ⁡ θ 3 ⋅ J   d r   d θ =

∫ 0 2 π ∫ 0 1 - 1 2 - 2 r cos ⁡ θ 3 ⋅ 6 r   d r d θ =

∫ 0 2 π ∫ 0 1 - 3 r - 4 r 2 cos ⁡ θ   d r d θ

Bora integrar?

Passo 11

∫ 0 2 π ∫ 0 1 - 3 r - 4 r 2 cos ⁡ θ   d r d θ = ∫ 0 2 π ∫ 0 1 - 3 r - 4 r 2 cos ⁡ θ   d r d θ =

∫ 0 2 π - 3 r 2 2 - 4 r 3 3 cos ⁡ θ 0 1 d θ = ∫ 0 2 π - 3 2 - 4 3 cos ⁡ θ   d θ =

- 3 2 θ - 4 3 sin ⁡ θ 0 2 π = - 3 π

Logo, pelo Teorema de Stokes:

∫ γ   F ⋅ d r → = - 3 π

Resposta

- 3 π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê