Seja a curva orientada parametrizada por:
Seja o campo vetorial:
Calcule:
Passo 1
Pela cara do campo vetorial, devemos aplicar Stokes, pois fazer a integral de linha não seria agradável. Como sabemos, o teorema de Stokes é utilizado quando conseguimos expressar o campo vetorial presente inicialmente, em campo rotacional, certo?
Além disso, vamos lembrar um pouco do que sabemos do Teorema de Stokes:
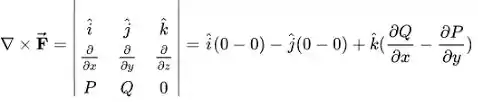
Logo, temos que o campo é de classe se por causa daquele expoente . Portanto temos que, pela Lei de Stokes:
Analisando a curva , vemos que para todo , que é o domínio dado no enunciado.
Substituindo por coordenadas cartesianas, temos que a curva está contida na superfície:
Vamos utilizar essa superfície na formula de Stokes.
Passo 2
Observamos que a projeção da curva no plano coordenado é um círculo de raio e tem o sentido anti-horário e, portanto, orientamos a superfície de forma compatível com o teorema de Stokes, isto é, com a terceira componente do vetor normal sendo positiva. Usando a parametrização natural, isto é, chamando a primeira coordenada de e a segunda de :
Temos que o domínio da parametrização é justamente a projeção dela no plano que vimos ali em cima que é um círculo de raio !
Temos também que o vetor normal é:
Que tem a orientação desejada.
Passo 3
Segue que:
Você precisa tomar cuidado ao olhar essa superfície, se fizer as contas você vai ver que ela é fechada, ou seja, começa e termina no mesmo ponto, mas como o rotacional é diferente de temos que fazer a conta como fazemos normalmente, isso porque com o rotacional diferente de não garantimos que a integral de linha é
Aplicando Stokes:
Aplicando coordenadas polares por causa do domínio e da integral:
Plugando a parametrização na definição do domínio :
Isto pois é positivo por definição.
Agora mudemos os diferenciais por jacobiano:
Passo 4
Plugando os limites e a parametrização na integral:
Em a integral é moleza, a outra é só um polinômio. Partiu pro abraço: