UFU, Sem Campus, Cálculo 1, Prof° Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 8.4b
Para cada uma das funções seguintes determine o(s) valor(es) de para o(s) qual(quais) a função é descontínua. identifique o(s) tipo(s) de descontinuidade(s). Nos casos possíveis, encontra uma nova definição para a função de modo a remover qualquer (quaisquer) descontinuidade(s) removível (removíveis).
Passo 1
Oiie, tudo certinho?
O enunciado nos dá a seguinte função
e pede para encontrarmos valores de para os quais tenhamos descontinuidades! Além disso, devemos identificar o tipo de descontinuidade, em geral, temos três tipos que irei apresentar. Primeiro, a descontinuidade removível, ela é tal que
está definida (ou não) e é um número real;
essa descontinuidade é tal que a função é descontínua apenas no ponto , não temos um salto da função, apenas um ponto deslocado, ela pode ser removida se redefinimos a função, e teremos que fazer isso se elas aparecerem! Agora, temos a descontinuidade de salto que é tal que
está definida (ou não) e é um número real;
ou seja, em um valor de , a função salta, tendo um espaço vazio no eixo . E, por último, temos a descontinuidade essencial
é uma assíntota vertical;
e são infinitos.
Vamos verificar qual o tipo de desigualdade em nossa função! Bora lá!
Passo 2
Primeiro, temos que nossa função é definida como
Esse tipo de função em geral poderia apresentar descontinuidades essenciais (com assíntotas verticais) se houvessem valores de no denominador da fração em que o polinômio se anulasse, ou seja, nas raízes de
usando Bhaskara, temos que
Ou seja, não temos raízes reais. Portanto, nenhuma descontinuidade essencial! Também temos uma razão de polinômios, portanto, não existem descontinuidades de salto, ou removíveis! O gráfico da função é tal que
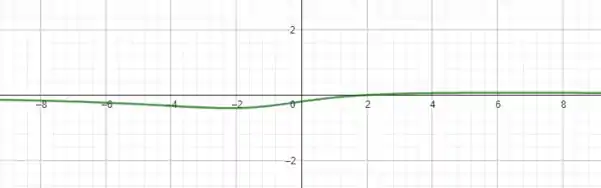
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Não há descontinuidades!