- Em cada item abaixo, esboce o gráfico de uma função f que satisfaz as condições do enunciado.
a) é contínua em todos os pontos, exceto em , onde o limite pela direita existe e é igual a .
Passo 1
Olá, galerinhaa!!! Vamos lá? Aqui nesta questão, vamos revisar alguns conteúdos de Cálculo 1, mais especificamente os conceitos de limite lateral direito e de continuidade.
A primeira coisa que temos que fazer é relembrar o que é limite lateral pela direita.
O limite lateral pela direita aparece quando nos aproximamos de um valor por meio de valores que são maiores que ele, ou seja, por valores que estão à direita dele na reta numérica, como mostra a figura abaixo

A sua notação é . Isso implica dizer que à medida que aproximamos x de , pela direita, os valores de se aproximam de .
Já o conceito de continuidade de uma função nos diz que uma função é contínua em um ponto se
- Existir
Passo 2
Vamos agora observar o gráfico abaixo
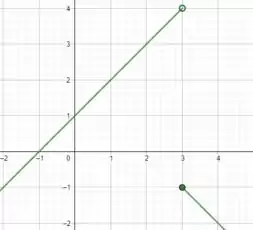
A função acima, dentro do intervalo que podemos ver, obedece aos critérios pedidos pela questão.
Se observarmos o gráfico, veremos que à medida que nos aproximamos de 3 pela direita o valor da imagem de se aproxima de -1, ou seja, . Também podemos notar, visualmente, que ela é contínua em todos os pontos, com exceção de (um jeito alternativo de olhar isso é perceber que a única “quebra” que aparece no esboço do gráfico ocorre nesse ponto).
Resposta
Ei, a resposta está no passo a passo :)