- Em cada item abaixo, esboce o gráfico de uma função f que satisfaz as condições do enunciado.
d) é contínua no intervalo , está definida em mas não é contínua em .
Passo 1
Olá, galerinhaa!!! Vamos lá? Aqui nesta questão, vamos revisar alguns conteúdos de Cálculo 1, mais especificamente o conceito de continuidade.
O conceito de continuidade de uma função nos diz que uma função é contínua em um ponto se
- Existir
Outra forma de entender a continuidade de uma função em um ponto é, olhando o gráfico dela, verificar se não há um “furo” ou uma “quebra” no desenho do gráfico da função.
Passo 2
Vamos agora observar o gráfico abaixo
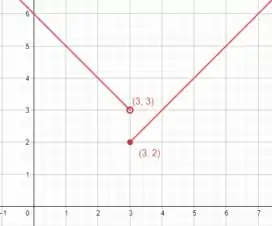
Pelo esboço acima, podemos ver que no intervalo , ou seja, em todos os valores reais maiores ou iguais a zero e menores que 3, a função é contínua, pois não tem “quebras”, em seu desenho.
Se olharmos em vamos ver que a função tem uma imagem definida que é . Isso nos garante que a função está definida (tem uma imagem para todo ponto) no intervalo .
Entretanto, a medida que partimos de e nos aproximamos de os valores em da imagem “caminham” para , mas ao chegarmos em notamos uma “ruptura” no gráfico e vemos que aí temos , valor diferente do esperado.
Então, por agora é isso, pessoal. Espero que tenham compreendido e até a próximaaa.
Resposta
Ei, a resposta está no passo a passo :)