Considere a função dada por
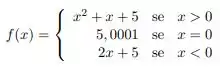
- Construa o gráfico de ;
Passo 1
Fala aí, beleza? Como vai a vida?
Sem enrolação, vamos fazer juntinhos mais uma questão?
O enunciado nos diz que é uma função com o domínio e o contradomínio estão contidos no conjunto dos números reais.
Não só, mas também pelo enunciado vemos que a função é uma função definida por partes. Em síntese, significa que de acordo com o intervalo que eu escolho a função muda a sua equação, ou seja, sua identidade se modifica. Assim, é muito importante se atentar para este fato quando esboçarmos cada trecho do nosso gráfico.
Passo 2
Então meu povo, como mencionado anteriormente a função em questão é uma função definida por partes. Isso significa que o nosso gráfico também será esboçado por partes.
De início, iremos pegar o intervalo onde . Se , então será : .
Nota-se a semelhança dessa função com a função genérica . Logo, para esse intervalo o esboço do gráfico será uma reta.
Além disso, utilizaremos do uso de uma tabela com o intuito de facilitar essa representação no plano cartesiano.
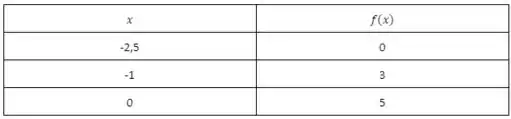
Traçando os pares ordenados da tabela acima, temos:
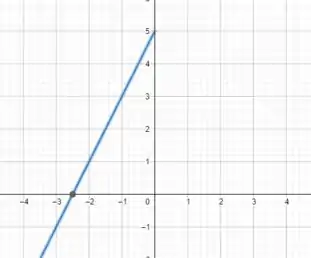
Passo 3
Agora, iremos fazer a mesma receitinha de bolo do passo anterior, porém modificando o intervalo.
Para , será : . O que isso quer dizer?
Significa que quando o , a função será constante e igual a . No esboço do gráfico, esse intervalo será representado pelo ponto de coordenadas ).
Passo 4
E por fim, temos o último intervalo que é quando , e o correspondente será : .
Logo, é possível observar que a equação desse intervalo possui similaridades com a função genérica .
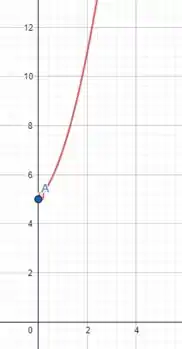
Dessa forma, constata-se que para esse intervalo a função assume a forma quadrática, sendo o seu esboço portanto, uma parabola.
Utilizaremos a tabela novamente para facilitar a marcação dos pares ordenados no plano cartesiano.
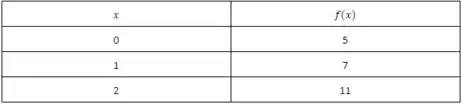
Assim, obtemos o esboço para esse intervalo:
Passo 5
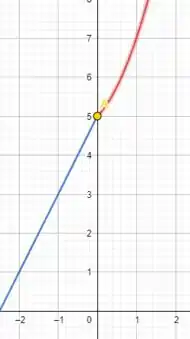
Essa é a hora de juntar todos os pedaços dos passos anteriores rs.

Obtemos assim o gráfico final:
E aí? Deu uma clareada nas ideias ai? Espero que sim!
Pois vem com a gente treinar mais um pouco! ;)
Resposta
Resolução nos passos acima