Considere a função dada por
![]()
- Construa o gráfico de ;
Passo 1
É um prazer ter vocês aqui novamente! E aí como anda os estudos por aí?
Bora resolver essa questão juntinhos?
O enunciado nos diz que é uma função com o domínio e o contradomínio estão contidos no conjunto dos números reais. Ademais, o enunciado fala que função é uma função definida por partes. Isso significa que de acordo com o intervalo que eu escolho a função muda de “cara”, ou seja, sua equação se modifica. Portanto, é muito importante ter atenção nesse fato quando esboçarmos cada trecho do nosso gráfico.
Passo 2
Bom gente, como já foi mencionado, a função é definida por partes. Logo, isso significa que o nosso gráfico também será esboçado por partes.

Primeiramente iremos pegar o intervalo onde . Se , então será :. Ora, ora aqui temos uma função modular, e isso foi perceptível pela presença do módulo na função. Ok?
Como queremos um jeito simples de fazer o gráfico para esse intervalo podemos utilizar uma tabela onde eu “chuto” valores para o e obtenha os respectivos valores para o
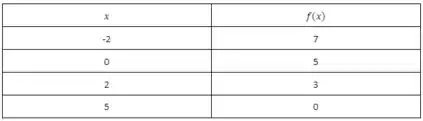
Nesse instante devemos marcar cada par ordenado no plano cartesiano e ligá-los de modo que se obtenha o esboço do gráfico para esse intervalo. Sendo assim, temos:
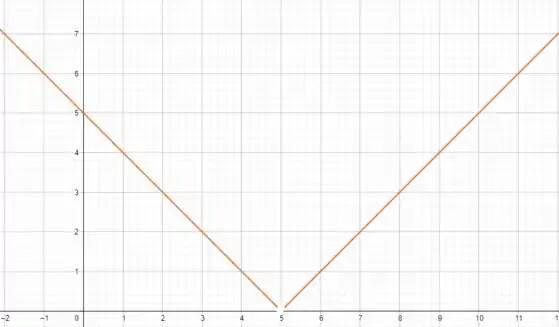
Passo 3
E por fim, temos o último intervalo que é quando , e o correspondente será . Consequentemente observa-se que quando o , a função é constante e igual a . Por isso, o esboço do gráfico para esse intervalo será apenas um ponto de coordenadas
Passo 4
Agora é a parte da cereja do bolo. hummm!

Vamos juntar os esboços dos passos anteriores e obter nosso gráfico final, assim temos que o gráfico terá o seguinte esboço final:
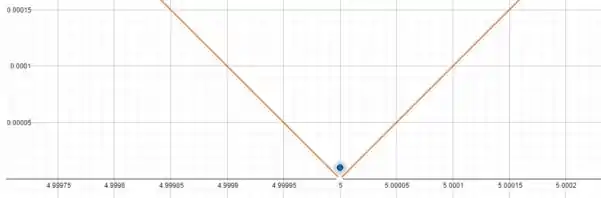
E aí? Tudo ok?
Pois vem com a gente treinar mais um pouco! ;)
Bons Estudos!
Resposta
Resolução nos passos acima